5．若a>0，b>0，且ln(a+b)＝0，则+的最小值是(　)

A. 　　　 　　　　　　　　　　 B．1

C．4　 　　　　　　　　 D．8

解析：由a>0，b>0，ln(a+b)＝0得.

故+＝＝≥＝＝4.

当且仅当a＝b＝时上式取“＝”．

答案：C

4．已知x＞1，y＞1，且lnx，，lny成等比数列，则xy(　)

A．有最大值e　 　　　　　　　 B．有最大值

C．有最小值e　 　　　　　　　 D．有最小值

解析：∵x>1，y>1，且lnx，，lny成等比数列，

∴lnx·lny＝≤²，

∴lnx+lny≥1⇒xy≥e.

答案：C

3．函数y＝(x>1)的最小值是(　)

A．2+2　 　　　　　　　　　　 B．2－2

C．2　 　　　　　　　　　 D．2

解析：∵x>1，∴x－1>0，

∴y＝＝

＝

＝

＝x－1++2

≥2·+2＝2+2，

当且仅当x－1＝，即x＝1+时，取等号．

答案：A

2．已知f(x)＝x+－2(x<0)，则f(x)有 (　)

A．最大值为0　 　　　　　　　 B．最小值为0

C．最大值为－4　 　　　　　　 D．最小值为－4

解析：∵x<0，∴－x>0，

∴x+－2＝－－2

≤－2·－2＝－4，

等号成立的条件是－x＝，即x＝－1.

答案：C

1．设a、b∈R，已知命题p：a²+b²≤2ab；命题q：()²≤，则p是q成立的

(　)

A．必要不充分条件　　　　　 B．充分不必要条件

C．充分必要条件　 　　　　　　　　 D．既不充分也不必要条件

解析：命题p：(a－b)²≤0⇔a＝b；命题q：(a－b)²≥0.显然，p⇒q，但q 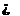p，则p是q的充分不必要条件．

答案：B

9．(2009·浙江高考)设等差数列{a_n}的前n项和为S_n，则S₄，S₈－S₄，S₁₂－S₈，S₁₆－S₁₂成等差数列．类比以上结论有：设等比数列{b_n}的前n项积为T_n，则T₄，_______，________，成等比数列．

解析：对于等比数列，通过类比，有等比数列{b_n}的前n项积为T_n，则T₄＝a₁a₂a₃a₄，T₈＝a₁a₂…a₈，T₁₂＝a₁a₂…a₁₂，T₁₆＝a₁a₂…a₁₆，因此＝a₅a₆a₇a₈，＝a₉a₁₀a₁₁a₁₂，＝a₁₃a₁₄a₁₅a₁₆，而T₄，，，的公比为q¹⁶，因此T₄，，，成等比数列．

8．方程f(x)＝x的根称为f(x)的不动点，若函数f(x)＝有唯一不动点，且x₁＝1 000，x_n+1＝(n∈N^*)，则x_{2 011}＝________.

解析：由＝x得ax²+(2a－1)x＝0.

因为f(x)有唯一不动点，

所以2a－1＝0，即a＝.

所以f(x)＝.所以x_n+1＝＝＝x_n+.

所以x_{2 011}＝x₁+×2 010＝1 000+＝2 005.

答案：2 005

7．在平面上，若两个正三角形的边长的比为1∶2，则它们的面积比为1∶4.类似地，在空间中，若两个正四面体的棱长的比为1∶2，则它们的体积比为________．

解析：＝＝()·＝×＝.

答案：1∶8

6．如图，椭圆中心在坐标原点，F为左焦点，当⊥时，其离心率为，此类椭圆被称为“黄金椭圆”．类比“黄金椭圆”，可推算出“黄金双曲线”的离心率e等于(　)

A. 　　　　　　　　　　 　　　 B.

C.－1　 　　　　　　　　　　　　 D.+1

解析：B(0，b)，F(－c,0)，A(a,0)．在“黄金双曲线”中，

∵⊥，∴·＝0.又＝(c，b)，＝(－a，b)．

∴b²＝ac.而b²＝c²－a²，∴c²－a²＝ac.

在等号两边同除以a²得e＝.

答案：A

5．由代数式的乘法法则类比推导向量的数量积的运算法则：

①“mn＝nm”类比得到“a·b＝b·a”；

②“(m+n)t＝mt+nt”类比得到“(a+b)·c＝a·c+b·c”；

③“(mn)t＝m(nt)”类比得到“(a·b)·c＝a·(b·c)”；

④“t≠0，mt＝xt⇒m＝x”类比得到“p≠0，a·p＝x·p⇒a＝x”；

⑤“|mn|＝|m||n|”类比得到“|a·b|＝|a|·|b|”；

⑥“＝”类比得到“＝”．

以上的式子中，类比得到的结论正确的个数是(　)

A．1　 　　　　　　　　 B．2

C．3　 　　　　　　　　 D．4

解析：只有①②对，其余错误．

答案：B