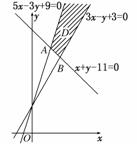
7．如果点P在平面区域上，点M的坐标为(3,0)，那么|PM|的最小值是________．

解析：点P所在的可行域如图中阴影部分(包括边界)所示，点M到A(1,1)，B(2，2)的距离分别为，，

又点M(3,0)到直线x－y＝0的距离为，故|PM|的最小值为.

6．设不等式组表示的平面区域为D.若指数函数y＝a^x的图象上存在区域D上的点，则a的取值范围是(　)

A．(1,3]　 　　　　　　　　　 B．[2,3]

C．(1,2] 　　　　　　　　　　 D．[3，+∞)

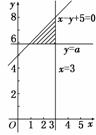
解析：画出不等式组表示的平面区域如图中阴影部分所示(包括边界)．当a>1时才能够使函数y＝a^x的图象上存在区域D上的点，由图可知当函数y＝a^x的图象经过点A时a取得最大值，

由方程组

解得x＝2，y＝9，即点A(2,9)，

代入函数解析式得9＝a²，

即a＝3，故1<a≤3.

答案：A

5．已知约束条件，若目标函数z＝x+ay(a≥0)恰好在点(2,2)处取得最大值，则a的取值范围为(　)

A．0＜a＜　 　　　　　　　　　　 B．a≥

C．a＞　 　　　　　　　　　　　　 D．0＜a＜

解析：画出已知约束条件的可行域为△ABC内部(包括边界)，如图，易知当a＝0时，不符合题意；当a＞0时，由目标函数z＝x+ay得y＝－x+，

则由题意得－3＝k_AC＜－＜0，

故a＞.综上所述，a＞.

答案：C

4．不等式组表示的平面区域是一个三角形，则a的范围是(　)

A．a<5 　　　　　　　　　　　　　　 　B．a≥8

C．5≤a＜8　 　　　　　　　　　　 　D．a＜5或a≥8

解析：如图所示，的交点为(0,5)，

的交点为(3,8)，∴5≤a＜8.

答案：C

3．设变量x，y满足约束条件则z＝2x+y的最大值为(　)

A．－2　　　　　　 B．4

C．6　 　　　　　　　　　　　　　　　　　　　 D．8

解析：在坐标平面内画出题中的不等式组表示的平面区域及直线2x+y＝0，平移该直线，当该直线经过该平面区域内的点(3,0)时，相应直线在x轴上的截距最大，此时z＝2x+y取得最大值，最大值是z＝2x+y＝2×3+0＝6.

答案：C

2．设D是由所确定的平面区域，记D被夹在直线x＝－1和x＝t(t∈[－1,1])间的部分的面积为S，则函数S＝f(t)的大致图象为(　)

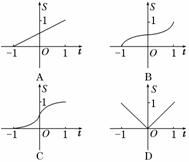
解析：如图，由不等式组画出平面区域．根据题意，由函数S＝f(t)的单调递增情况易选出答案B.

答案：B

1．不等式(x－2y+1)(x+y－3)≤0在坐标平面内表示的区域(用阴影部分表示)应是

　(　)

解析：(x－2y+1)(x+y－3)≤0

⇔或

结合图形可知选C.

答案：C

8．已知函数f(x)＝x+(p为常数，且p>0)，若f(x)在(1，+∞)上的最小值为4，则实数p的值为________．

解析：由题意得x－1>0，f(x)＝x－1++1≥2+1，当且仅当x＝+1时，取等号，则2+1＝4，

解得p＝.

7．(2010·南京模拟)若log_mn＝－1，则3n+m的最小值是________．

解析：∵log_mn＝－1，∴m^－1＝n，∴mn＝1，

∵n＞0，m＞0且m≠1，∴3n+m≥2＝2.

当且仅当3n＝m，即n＝，m＝时等号成立．

答案：2

6．某商场中秋前30天月饼销售总量f(t)与时间t(0<t≤30)的关系大致满足f(t)＝t²+10t+16，则该商场前t天平均售出(如前10天的平均售出为)的月饼最少为(　)

A．18　 　　　　　　　　　　　 B．27

C．20　 　　　　　　　　　　　 D．16

解析：平均销售量y＝＝＝t++10≥18.

当且仅当t＝，即t＝4∈[1,30]等号成立，

即平均销售量的最小值为18.

答案：A