7．已知m、n是不同的直线，α、β是不重合的平面，给出下列命题：

①若m∥α，则m平行于平面α内的无数条直线；

②若α∥β，m⊂α，n⊂β，则m∥n；

③若m⊥α，n⊥β，m∥n，则α∥β；

④若α∥β，m∥α，则m∥β.

其中，真命题的序号是________(写出所有真命题的序号)．

解析：由线面平行定义及性质知①正确．②中若m⊂α，n⊂β，α∥β，

则m、n可能平行，也可能异面，故②错，

③中由⇒⇒α∥β知③正确．

④中由α∥β，m∥α可得，m∥β或m⊂β，故④错．

答案：①③

6.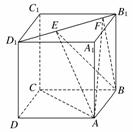如图，正方体ABCD－A₁B₁C₁D₁的棱长为1，线段B₁D₁上有两个动点E、F，且EF＝，则下列结论中错误的是(　)

A．AC⊥BE

B．EF∥平面ABCD

C．三棱锥A－BEF的体积为定值

D．△AEF的面积与△BEF的面积相等

解析：由AC⊥平面DBB₁D₁可知AC⊥BE.故A正确．

EF∥BD，EF⊄平面ABCD，BD⊂平面ABCD，知EF∥平面ABCD，故B正确．

A到平面BEF的距离即为A到平面DBB₁D₁的距离，为，且S_△BEF＝BB₁×EF＝定值，

故V_A－BEF为定值，即C正确．

答案：D

5．(2010·无锡一模)下列命题中正确的个数是(　)

①若直线a不在α内，则a∥α；

②若直线l上有无数个点不在平面α内，则l∥α；

③若直线l与平面α平行，则l与α内的任意一条直线都平行；

④若l与平面α平行，则l与α内任何一条直线都没有公共点；

⑤平行于同一平面的两直线可以相交．

A．1　 　　　　　　　　 　B．2

C．3　 　　　　　　　　 　D．4

解析：a∩α＝A时，a⊄α，∴①错；

直线l与α相交时，l上有无数个点不在α内，故②错；

l∥α时，α内的直线与l平行或异面，故③错；

l∥α，l与α无公共点，∴l与α内任一直线都无公共点，④正确；

长方体中A₁C₁与B₁D₁都与面ABCD平行，

∴⑤正确．

答案：B

4．给出下列命题：

①若直线a∥直线b，且直线a∥平面α，则直线b与平面α的位置关系是平行或直线b在平面α内；

②直线a∥平面α，平面α内有n条直线交于一点，那么这n条直线中与直线a平行的直线有且只有一条；

③a∥α，b、c⊂α，a∥b，b⊥c，则有a⊥c；

④过平面外一点只能引一条直线与这个平面平行；

其中错误的个数是(　)

A．0　 　　　　　　　　　　　　 B．1

C．2　 　　　　　　　　　　　　 D．3

解析：②④错误．

答案：C

3．下列命题正确的是(　)

A．直线a与平面α不平行，则直线a与平面α内的所有直线都不平行

B．如果两条直线在平面α内的射影平行，则这两条直线平行

C．垂直于同一直线的两个平面平行

D．直线a与平面α不垂直，则直线a与平面α内的所有直线都不垂直

解析：当直线a在平面α内时，它与平面α不平行，但a可以与平面α内的一些直线平行，故选项A错误；两条直线在平面α内的射影平行，则可以为异面直线，故选项B错误；直线a与平面α不垂直，但直线a可以与平面α内的一些直线垂直，故选项D错误，只有选项C正确．

答案：C

2．(2010·江南十校)已知a、b、l表示三条不同的直线，α、β、γ表示三个不同的平面，有下列四个命题：

①若α∩β＝a，β∩γ＝b且a∥b，则α∥γ；

②若a、b相交，且都在α、β外，a∥α，a∥β，b∥α，b∥β，则α∥β；

③若α⊥β，α∩β＝a，b⊂β，a⊥b，则b⊥α；

④若a⊂α，b⊂α，l⊥a，l⊥b，则l⊥α.

其中正确的是(　)

A．①②　　　　　B．②③

C．①④　 　　　　　　　　　　　　 　D．③④

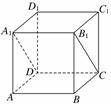解析：可通过公理、定理判定其正确，通过特例、反例说明其错误．①在正方体A₁B₁C₁D₁－ABCD中，平面A₁B₁CD∩平面DCC₁D₁＝CD.平面A₁B₁C₁D₁∩平面DCC₁D₁＝C₁D₁，且CD∥C₁D₁，但平面A₁B₁CD与平面A₁B₁C₁D₁不平行，①错误．②因为a、b相交，可设其确定的平面为γ，根据a∥α，b∥α，可得γ∥α.同理可得γ∥β，因此α∥β，②正确．③根据平面与平面垂直的判定定理：两平面垂直，在一个平面内垂直于交线的直线和另一个平面垂直，③正确．④当直线a∥b时，l垂直于平面α内两条不相交直线，得不出l⊥α，④错误．

答案：B

1．(2010·湖南四县调研)平面α∥平面β的一个充分条件是(　)

A．存在一条直线a，a∥α，a∥β

B．存在一条直线a，a⊂α，a∥β

C．存在两条平行直线a，b，a⊂α，b⊂β，a∥β，b∥α

D．存在两条异面直线a，b，a⊂α，b⊂β，a∥β，b∥α

解析：A、B、C中α与β都有可能相交．

答案：D

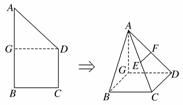
12．(2010·茂名模拟)如图所示，在直角梯形ABCD中，∠B＝90°，DC∥AB，CD＝AB，G为线段AB的中点，将 △ADG沿GD折起，使平面ADG⊥平面BCDG，得到几何体A－BCDG.

(1)若E，F分别为线段AC，AD的中点，求证：EF∥平面ABG；

(2)求证：AG⊥平面BCDG.

证明：(1)依题意，折叠前后CD、BG的位置关系不改变，

∴CD∥BG.

∵E、F分别为线段AC、AD的中点，

∴在△ACD中，EF∥CD，∴EF∥BG.

又EF⊄平面ABG，BG⊂平面ABG，∴EF∥平面ABG.

(2)将△ADG沿GD折起后，AG、GD的位置关系不改变，

∴AG⊥GD.

又平面ADG⊥平面BCDG，平面ADG∩平面BCDG＝GD，AG⊂平面AGD，

∴AG⊥平面BCDG.

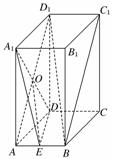
11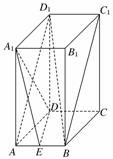．(2010·北京海淀)如图，长方体ABCD－A₁B₁C₁D₁中，AB＝1，AA₁＝AD＝2.点E为AB中点．

(1)求三棱锥A₁－ADE的体积；

(2)求证：A₁D⊥平面ABC₁D₁；

(3)求证：BD₁∥平面A₁DE.

解：(1)在长方体ABCD－A₁B₁C₁D₁

中，

因为AB＝1，E为AB的中点，

所以，AE＝.

又因为AD＝2，

所以S_△ADE＝AD·AE＝×2×＝.

又AA₁⊥底面ABCD，AA₁＝2，

所以三棱锥A₁－ADE的体积

V＝S_△ADE·AA₁＝××2＝.

(2)证明：因为AB⊥平面ADD₁A₁，

A₁D⊂平面ADD₁A₁，

所以AB⊥A₁D.

因为ADD₁A₁为正方形，

所以AD₁⊥A₁D.

又AD₁∩AB＝A，

AD₁⊂平面ABC₁D₁，AB⊂平面ABC₁D₁，

所以A₁D⊥平面ABC₁D₁.

(3)证明：设AD₁，A₁D的交点为O，连结OE.

因为ADD₁A₁为正方形，

所以O是AD₁的中点，

在△AD₁B中，OE为中位线，

所以OE∥BD₁.

又OE⊂平面A₁DE，BD₁⊄平面A₁DE，

所以BD₁∥平面A₁DE.

10．(2010·山东临沂)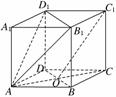在直平行六面体AC₁中，四边形ABCD是菱形，∠DAB＝60°，AC∩BD＝O，AB＝AA₁.

(1)求证：C₁O∥平面AB₁D₁；

(2)求证：平面AB₁D₁⊥平面

ACC₁A₁.

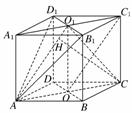证明：(1)连接A₁C₁交B₁D₁于O₁，连接AO₁.

在平行四边形AA₁C₁C中，C₁O₁∥AO，C₁O₁＝AO，

∴四边形AOC₁O₁为平行四边形，

∴C₁O∥AO₁.

∵C₁O⊄平面AB₁D₁，AO₁⊂平面AB₁D₁，

∴C₁O∥平面AB₁D₁.

(2)在直平行六面体AC₁中，A₁A⊥平面A₁B₁C₁D₁，

∴A₁A⊥B₁D₁.

∵四边形A₁B₁C₁D₁为菱形，∴B₁D₁⊥A₁C₁.

∵A₁C₁∩AA₁＝A₁，A₁C₁⊂平面ACC₁A₁，AA₁⊂平面ACC₁A₁，

∴B₁D₁⊥平面ACC₁A₁.

∵B₁D₁⊂平面AB₁D₁，∴平面AB₁D₁⊥平面ACC₁A₁.