6．正方体ABCD－A₁B₁C₁D₁中，P、Q、R分别是AB、AD、B₁C₁的中点．那么，正方体的过P、Q、R的截面图形是(　)

A．三角形　 　　　　　　　　　　　　　　 B．四边形

C．五边形　 　　　　　　　　　　　　　　 D．六边形

解析：边长是正方体棱长的倍的正六边形．

答案：D

5．(2010·中山模拟)设四棱锥P－ABCD的底面不是平行四边形，用平面α去截此四棱锥(如图)，使得截面四边形是平行四边形，则这样的平面α(　)

A．不存在　 　　　　　　　　　　 B．只有1个

C．恰有4个　 　　　　　 D．有无数多个

解析：设四棱锥的两组不相邻的侧面的交线为m、n，直线m、n确定了一个平面β.作与β平行的平面α，与四棱锥的各个侧面相截，则截得的四边形必为平行四边形．而这样的平面α有无数多个．

答案：D

4．在正方体ABCD－A₁B₁C₁D₁中，E、F分别为棱AA₁、CC₁的中点，则在空间中与三条直线A₁D₁、EF、CD都相交的直线(　)

A．不存在　 　　　　　　　　　　　　　　　　　 B．有且只有两条

C．有且只有三条　 　　　　　　　　 D．有无数条

解析：过直线A₁D₁可做无数个平面与直线EF、CD相交，则其交点的连线必与直线A₁D₁相交，故可有无数条直线与三条直线同时相交．

答案：D

3．如图，α∩β＝l，A、B∈α，C∈β，C∉l，直线AB∩l＝M，过A、B、C三点的平面记作γ，则γ与β的交线必通过(　)

A．点A　　　　　 B．点B

C．点C但不过点M　 　　　　　　 D．点C和点M

解析：通过A、B、C三点的平面γ，即是通过直线AB与点C的平面，M∈AB.∴M∈γ，而C∈γ，又∵M∈β，C∈β.∴γ和β的交线必通过点C和点M.

答案：D

2．下列说法正确的是(　)

A．如果两个不重合的平面α、β有一条公共直线a，就说平面α、β相交，并记作α∩β＝a

B．两个平面α、β有一个公共点A，就说α、β相交于过A点的任意一条直线

C．两个平面α、β有一个公共点A，就说α、β相交于A点，并记作α∩β＝A

D．两个平面ABC与DBC相交于线段BC

解析：根据平面的性质公理3可知，A对；对于B，其错误在于“任意”二字上；对于C，错误在于α∩β＝A上；对于D，应为平面ABC和平面DBC相交于直线BC.

答案：A

1．已知a、b是异面直线，直线c∥直线a，则c与b(　)

A．一定是异面直线　　　　　　　　 B．一定是相交直线

C．不可能是平行直线　 　　　　　　　　 D．不可能是相交直线

解析：c与b不可能是平行直线，否则与条件矛盾．

答案：C

12．(2010·山东济南)如图，棱柱ABCD－A₁B₁C₁D₁的底面ABCD为菱形，平面AA₁C₁C⊥平面ABCD.

(1)证明：BD⊥AA₁；

(2)证明：平面AB₁C∥平面

DA₁C₁；

(3)在直线CC₁上是否存在点P，使BP∥平面DA₁C₁？若存在，求出点P的位置；若不存在，说明理由．

解：(1)证明：连接BD，

∵平面ABCD为菱形，

∴BD⊥AC，

由于平面AA₁C₁C⊥平面ABCD，

则BD⊥平面AA₁C₁C，

又A₁A⊂平面AA₁C₁C，

故BD⊥AA₁.

(2)证明：由棱柱ABCD－A₁B₁C₁D₁的性质知AB₁∥DC₁，A₁D∥B₁C，

AB₁∩B₁C＝B₁，A₁D∩DC₁＝D，

由面面平行的判定定理推论知：平面AB₁C∥平面DA₁C₁.

(3)存在这样的点P满足题意．

∵A₁B₁綊AB綊DC，

∴四边形A₁B₁CD为平行四边形．

∴A₁D∥B₁C，

在C₁C的延长线上取点P，使C₁C＝CP，连接BP，

∵B₁B綊CC₁，∴BB₁綊CP，

∴四边形BB₁CP为平行四边形，

∴BP∥B₁C，∴BP∥A₁D，

∴BP∥平面DA₁C₁.

求证：EF∥平面SAD.

证明：法一：作FG∥DC交SD于点G，则G为SD的中点．

连结AG，FG綊CD，

又CD綊AB，且E为AB的中点，

故FG綊AE，

∴四边形AEFG为平行四边形．

∴EF∥AG.

又∵AG⊂平面SAD，EF⊄平面SAD，

∴EF∥平面SAD.

法二：取线段CD的中点M，连结ME，MF，

∵E，F分别为AB，SC的中点，

∴ME∥AD，MF∥SD，

又∵ME，MF⊄平面SAD，

∴ME∥平面SAD，MF∥平面SAD

又∵ME，MF相交，

∴平面MEF∥平面SAD，

∵EF⊂平面MEF，

∴EF∥平面SAD.

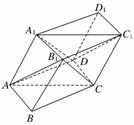
11.如图，已知α∥β，异面直线AB、CD和平面α、β分别交于A、B、C、D四点，E、F、G、H分别是AB、BC、CD、DA的中点．

求证：(1)E、F、G、H共面；

(2)平面EFGH∥平面α.

证明：(1)∵E、H分别是AB、DA的中点，

∴EH∥BD且EH＝BD.

同理，FG∥BD且FG＝BD，

∴FG∥EH且FG＝EH.

∴四边形EFGH是平行四边形，即E、F、G、H共面．

(2)平面ABD和平面α有一个公共点A，

设两平面交于过点A的直线AD′.

∵α∥β，∴AD′∥BD.

又∵BD∥EH，∴EH∥BD∥AD′.

∴EH∥平面α，

同理，EF∥平面α，

又EH∩EF＝E，EH⊂平面EFGH，

EF⊂平面EFGH，

∴平面EFGH∥平面α.

9．如图，在正四棱柱ABCD－A₁B₁C₁D₁中，E、F、G、H分别是棱CC₁、C₁D₁、D₁D、DC的中点，N是BC的中点，点M在四边形EFGH及其内部运动，则当M满足条件________________时，有MN∥平面B₁BDD₁.

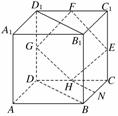
解析：当M点满足在线段FH上有MN∥面B₁BDD₁.

答案：M∈线段FH

8．正方体ABCD－A₁B₁C₁D₁中，E是DD₁的中点，则BD₁与平面ACE的位置关系为 ________.

解析：如图，连结AC、BD交于O，连结EO，则EO∥BD₁

又EO⊂面ACE，故BD₁∥面ACE.

答案：平行