2．设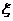是一个离散型随机变量，其分布列如下表，求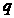的值

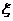	－1	0	1
P		1－2

　解：因为随机变量的概率非负且随机变量取遍所有可能值时相应的概率之和等于1，所以解得。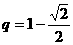

★ 抢 分 频 道 ★

基础巩固训练

1．设随机变量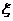的分布列为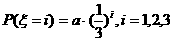，则a的值为(　 )

A .1；　 B.9/13；　 C.11/13；　　 D.27/13

答案：D

2．(广东省五校2008年高三上期末联考)一个盒子装有六张卡片，上面分别写着如下六个定义域为R的函数：

现从盒子中进行逐一抽取卡片，且每次取出后均不放回，若取到一张记有偶函数的卡片则停止抽取，否则继续进行，求抽取次数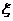的分布列和数学期望.

解：　 ξ可取1，2，3，4.

　　 ，

　　 ； …………8分

　　 故ξ的分布列为

ξ	1	2	3	4
P

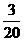考点二: 离散型随机变量分布列的性质

题型1: 离散型随机变量分布列的性质的应用

	0	1	2	3
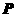	0.1			0.1

　[例3] (四川省乐山市2008届第一次调研考试)某一随机变量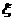的概率分布如下表，且，则的值为(　　)

　A.－0.2；　　B.0.2；　　C.0.1；　　D.－0.1

[解题思路]： 由离散型随机变量分布列的性质可得

解析：由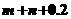，又，可得

答案：B

[名师指引]离散型随机变量的分布列都具有下面两个性质：

⑴P_i≥0，i＝1，2，…；　　

⑵P₁+P₂+…=1．

[新题导练]

1. (安徽省淮南市2008届高三第一次模拟考试)某校设计了一个实验学科的实验考查方案：考生从6道备选题中一次性随机抽取3题，按照题目要求独立完成全部实验操作.　 规定：至少正确完成其中2题的便可提高通过.　 已知6道备选题中考生甲有4题能正确完成，2题不能完成；考生乙每题正确完成的概率都是，且每题正确完成与否互不影响.分别写出甲、乙两考生正确完成题数的概率分布列；

解：设考生甲、乙正确完成实验操作的题数分别为、，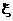

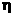则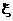取值分别为1，2，3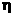；取值分别为0，1，2，3。…………………………………2分

，，。

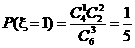∴考生甲正确完成题数的概率分布列为

	1	2	3

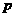2．.随机变量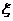的所有等可能取值为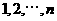，若，则(　　 )

A．；　B．；　C．；　D．不能确定

答案：C

题型2。离散型随机变量分布列的计算

[例2] (2008广东省广州执信中学、中山纪念中学、深圳外国语学校三校期末联考)旅游公司为3个旅游团提供4条旅游线路，每个旅游团任选其中一条.求选择甲线路旅游团数的分布列.

[解题思路]：求3个旅游团选择3条不同的线路的概率,　 再按定义求红球的分布列.

解析： 设选择甲线路旅游团数为ξ，则ξ=0，1，2，3

　　 P(ξ=0)=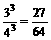　　　 P(ξ=1)=

　　 P(ξ=2)= 　　　P(ξ=3)= 　

　　 ∴ξ的分布列为：

ξ	0	1	2	3
P

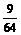[名师指引] 求离散型随机变量分布列时，应明确随机变量可能取哪些值，然后计算其相应的概率填入相应的表中即可。

[新题导练]

1．抛掷两颗骰子，所得点数之和为ξ，那么ξ=4表示的随机试验结果是

A.一颗是3点，一颗是1点

B.两颗都是2点

C.两颗都是4点

D.一颗是3点，一颗是1点或两颗都是2点

答案：D　 解析：对A、B中表示的随机试验的结果，随机变量均取值4，而D是 ξ=4代表的所有试验结果.掌握随机变量的取值与它刻画的随机试验的结果的对应关系是理解随机变量概念的关键.

3.重难点：.

问题1: 　离散型随机变量与连续型随机变量的区别与联系:

点拨：离散型随机变量与连续型随机变量都是用变量表示随机试验的结果；但是离散型随机变量的结果可以按一定次序一一列出，而连续性随机变量的结果不可以一一列出

　 注意：(1)有些随机试验的结果虽然不具有数量性质，但可以用数量来表达如投掷一枚硬币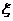，=0，表示正面向上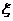，=1，表示反面向上

(2)若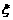是随机变量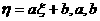，是常数，则也是随机变量

★ 热 点 考 点 题 型 探 析★

考点一：离散型随机变量及其分布列的计算

题型1. 离散型随机变量的取值

[例1] 写出下列随机变量可能取的值，并说明随机变量所取的值表示的随机试验的结果

(1)一袋中装有5只同样大小的白球，编号为1，2，3，4，5 现从该袋内随机取出3只球，被取出的球的最大号码数ξ；

　　 (2)某单位的某部电话在单位时间内收到的呼叫次数η

　[解题思路]： 注意事件与数字间的对应关系。

解析： (1) ξ可取3，4，5

　　 ξ=3，表示取出的3个球的编号为1，2，3；

　　 ξ=4，表示取出的3个球的编号为1，2，4或1，3，4或2，3，4；

ξ=5，表示取出的3个球的编号为1，2，5或1，3，5或1，4，5或2，3或3，4，5

　　 (2)η可取0，1，…,n，…

　　 η=i，表示被呼叫i次，其中i=0,1,2,…

[名师指引]离散型随机变量的取值可以一一列举，当可取值较多时也可采用类似(2)的表示方法。

[新题导练]

2.难点：会求某些简单的离散型随机变量的分布列；掌握离散型随机变量的分布列的两个基本性质及简单运用。

1.重点：了解随机变量、离散型随机变量、连续型随机变量及离散型随机变量的分布列的意义，

5. 分布列的两个性质：任何随机事件发生的概率都满足:，并且不可能事件的概率为0，必然事件的概率为1．由此你可以得出离散型随机变量的分布列都具有下面两个性质：

⑴_____________.

⑵_____________.

答案：P_i≥0，i＝1，2，…；　 P₁+P₂+…=1．

特别提醒：对于离散型随机变量在某一范围内取值的概率等于它取这个范围内各个值的概率的和 即

★ 重 难 点 突 破 ★