
题目列表(包括答案和解析)
3. 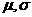 是参数
是参数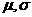 是参数的意义:
是参数的意义:
① ______________________;
② ______________________’
答案:
①
当 一定时,曲线随
一定时,曲线随 质的变化沿x轴平移;
质的变化沿x轴平移;
②
当 一定时,曲线形状由
一定时,曲线形状由 确定:
确定: 越大,曲线越“矮胖”,表示总体分布越集中;
越大,曲线越“矮胖”,表示总体分布越集中;
 越小,曲线越“高瘦”,表示总体分布越分散。
越小,曲线越“高瘦”,表示总体分布越分散。
特别提醒:
(1)P =0.6826;
=0.6826;
(2)P =0.9544
=0.9544
 (3)P
(3)P =0.9974
=0.9974
2.正态曲线的性质:
① ______________________;
② ______________________;
③ ______________________;
④ ______________________;
答案:
① 曲线位于x轴上方,与x轴不相交;
②
曲线是单峰的,关于直线x= 对称;
对称;
③
曲线在x= 处达到峰值
处达到峰值 ;
;
④ 曲线与x轴之间的面积为1;
1. 正态总体的概率密度函数: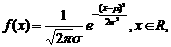 式中
式中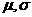 是参数,分别表示___________与___________;
是参数,分别表示___________与___________;
当 时得到标准正态分布密度函数:
时得到标准正态分布密度函数: .
.
答案: 总体的平均数(期望值); 标准差
10.2009年广东省广州市高三年级调研测试(理 科)
一厂家向用户提供的一箱产品共10件,其中有2件次品,用户先对产品进行抽检以决定是否接收.
抽检规则是这样的:一次取一件产品检查(取出的产品不放回箱子),若前三次没有抽查到次品,
则用户接收这箱产品;若前三次中一抽查到次品就立即停止抽检,并且用户拒绝接收这箱产品.
(1)求这箱产品被用户接收的概率;
(2)记抽检的产品件数为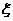 ,求
,求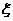 的分布列和数学期望.
的分布列和数学期望.
解:(1)设“这箱产品被用户接收”为事件 ,
,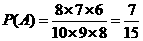 .
.
即这箱产品被用户接收的概率为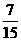 .
.
(2)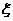 的可能取值为1,2,3.
的可能取值为1,2,3.
 =
= ,
,
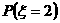 =
= ,
,
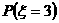 =
= ,
,
∴ 的概率分布列为:
的概率分布列为:
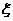 |
1 |
2 |
3 |
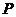 |
 |
 |
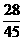 |
∴ =
=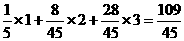 .
.
9.广东省普宁市城东中学2009届高三上学期第三次月考(数学理)
交5元钱,可以参加一次摸奖。一袋中有同样大小的球10个,其中有8个标有1元钱,2个标有5元钱,摸奖者只能从中任取2个球,他所得奖励是所抽2球的钱数之和(设为ξ),求抽奖人获利的数学期望。
解:因为ξ为抽到的2球的钱数之和,则ξ可能取的值为2,6,10.
且P(ξ=2)= P(ξ=6)=
P(ξ=6)= P(ξ=10)=
P(ξ=10)=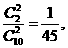
∴Eξ=2×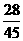 +6×
+6× +10×
+10× =
= =
=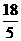 ,
,
又设η为抽奖者获利的可能值,则η=ξ-5,
∴抽奖者获利的数学期望为 Eη=E(ξ-5)=Eξ-5=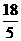 -5=-
-5=-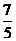 ,
,
答:抽奖人获利的期望为-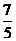 .
.
8.2008学年中山市一中高三年级第一次统测试题理科数学
交5元钱,可以参加一次抽奖。一袋中有同样大小的球10个,其中有8个标有1元,
2个标有5元,摸奖者只能从中任取2个球,他所得奖励是所抽2球标的钱数之和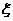 。
。
(I)求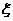 的概率分布列; (II)求抽奖人获利的数学期望。
的概率分布列; (II)求抽奖人获利的数学期望。
解(I) ……………………………………………………2分
……………………………………………………2分
 ,
,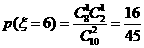 ,
, ……8分
……8分
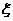 |
2 |
6 |
10 |
 |
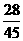 |
 |
 |
所以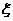 的概率分布列为:
的概率分布列为:
………………………10分
(II)由(I)知,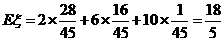 ………………………12分
………………………12分
所以抽奖人获利的数学期望为: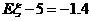 元。 ………………………14分
元。 ………………………14分
7.广东中山桂山中学2009届高三月考数学(理)试卷
甲、乙两人各射击一次,击中目标的概率分别是 和
和 .假设两人射击是否击中目标,相互之间没有影响;每次射击是否击中目标,相互之间没有影响.
.假设两人射击是否击中目标,相互之间没有影响;每次射击是否击中目标,相互之间没有影响.
(Ⅰ)甲射击4次,至少1次未击中目标的概率________________;
(Ⅱ) 求两人各射击4次,甲恰好击中目标2次且乙恰好击中目标3次的概率_________;
(Ⅲ) 假设某人连续2次未击中目标,则停止射击. 问: 乙恰好射击5次后,被中止射击的概率是____________
答案:(1)  (2)
(2) 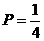 (3)
(3) 
6.已知随机变量的分布列是
|
ξ |
1 |
2 |
3 |
|
P |
0.4 |
0.2 |
0.4 |
则Dξ=____________;
答案:0.8
综合拔高训练
5.(广东省揭阳市2008年高中毕业班高考调研测试)一个篮球运动员投篮一次得3分的概率为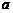 ,得2分的概率为
,得2分的概率为 ,不得分的概率为
,不得分的概率为 (
(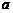 、
、 、
、 ),已知他投篮一次得分的数学期望为2(不计其它得分情况),则
),已知他投篮一次得分的数学期望为2(不计其它得分情况),则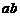 的最大值为
的最大值为
A. B.
B. C.
C.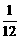 D.
D.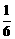
答案:由已知得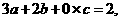 即
即
 ,故选D.
,故选D.
4.(安徽省蚌埠二中2008届高三8月月考)设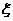 是离散型随机变量,
是离散型随机变量, ,
,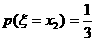 ,且
,且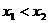 ,现已知:
,现已知: ,
,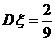 ,则
,则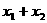 的值为
的值为
(A) (B)
(B) (C) 3 (D)
(C) 3 (D)  答案:C
答案:C
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com