
题目列表(包括答案和解析)
4.下列函数是正态分布密度函数的是( )
A.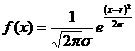 B.
B.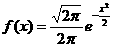
C.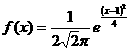 D.
D.
答案:B
3.正态分布有两个参数 与
与 ,( )相应的正态曲线的形状越扁平。
,( )相应的正态曲线的形状越扁平。
A. 越大 B.
越大 B. 越小 C.
越小 C. 越大 D.
越大 D. 越小
越小
答案:C
2.标准正态分布的均数与标准差分别为( )。
A.0与1 B.1与0 C.0与0 D.1与1
答案:A
1. 正态曲线是
A.递增函数 B.递减函数 C.从左到右先增后减的函数 D.从左到右先减后增的函数
答案:C
2.如果随机变量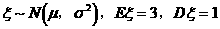 ,则
,则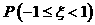 等于()
等于()
A. B.
B.
C.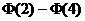 D.
D.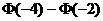
答案:B 解析:这里的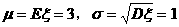
由换算关系式 ,有
,有
★ 抢 分 频 道 ★
基础巩固训练
1. 正态总体为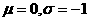 概率密度函数
概率密度函数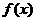 是( )
是( )
A.奇函数 B.偶函数 C.非奇百偶函数 D.既是奇函数又是偶函数
答案:B
3.重难点:.
(1) 正态分布与正态曲线
问题1:若总体密度曲线就是或近似地是函数 的图象,则其分布叫正态分布,常记作
的图象,则其分布叫正态分布,常记作 .
.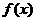 的图象称为正态曲线.
的图象称为正态曲线.
点拨:画出三条正态曲线:即①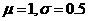 ;②
;② ;③
;③ ,其图象如下图所示:
,其图象如下图所示:

观察以上三条正态曲线,得以下性质:
①曲线在x轴的上方,与x轴不相交.
②曲线关于直线 对称,且在
对称,且在 时位于最高点.
时位于最高点.
③当 时,曲线上升;当
时,曲线上升;当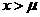 时,曲线下降.并且当曲线向左、右两边无限延伸时,以x轴为渐近线,向它无限靠近.
时,曲线下降.并且当曲线向左、右两边无限延伸时,以x轴为渐近线,向它无限靠近.
④当 一定时,曲线的形状由
一定时,曲线的形状由 确定.
确定. 越大,曲线越“矮胖”,表示总体的分布越分散;
越大,曲线越“矮胖”,表示总体的分布越分散; 越小,曲线越“瘦高”,表示总体的分布越集中.
越小,曲线越“瘦高”,表示总体的分布越集中.
注意: 当 时,正态总体称为标准正态总体,相应的函数表示式是
时,正态总体称为标准正态总体,相应的函数表示式是 .相应的曲线称为标准正态曲线.
.相应的曲线称为标准正态曲线.
★ 热 点 考 点 题 型 探 析★
考点一: 正态分布的应用
题型1. 正态分布公式的应用
[例1] 给出下列三个正态总体的函数表达式,请找出其均值μ和标准差σ 
(1)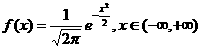
(2)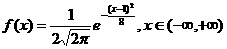
(3)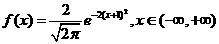
[解题思路]:考查正态总体的概率密度函数公式, 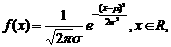 式中
式中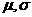 是参数,分别表示总体的平均数(期望值)与标准差
是参数,分别表示总体的平均数(期望值)与标准差
解析:(1)0,1;(2)1,2;(3)-1,0.5 
[例2] 某物体的温度 (
( )是一个随机变量,已知
)是一个随机变量,已知 ,又随机变量
,又随机变量 (
( )
)
满足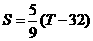 ,求
,求 的概率密度。
的概率密度。
[解题思路]: 为华氏度,。C为摄氏度。
为华氏度,。C为摄氏度。 为
为 的线性函数,由要点4知
的线性函数,由要点4知 也服从正态分布,再由要点1求出
也服从正态分布,再由要点1求出 的概率密度。
的概率密度。
解析: 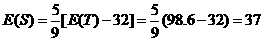

所以随机变量 的概率密度为
的概率密度为

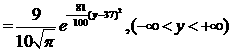
[例3] 灯泡厂生产的白炽灯寿命ξ(单位:h),已知ξ-N(1000,302),要使灯泡的平均寿命为1000h的概率为99.7%,问灯泡的最低使用寿命应控制在多少小时以上?
[解题思路]:进行假设检验的方法与步骤:
(1)提出统计假设,具体问题里的统计假设服从正态分布N(μ,σ2);
(2)确定一次试验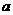 值是否落入(μ-3σ,μ+3σ);
值是否落入(μ-3σ,μ+3σ);
(3)作出判断:如果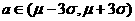 ,就接受假设;如果
,就接受假设;如果 ,由于这是小概率事件,就拒绝假设,说明生产过程中出现了异常情况
,由于这是小概率事件,就拒绝假设,说明生产过程中出现了异常情况
解析:解:因为灯泡寿命ξ-N(1000,302),故ξ在(1000-3×30,1000+3×30)内取值的概率为99.7%,即在(910,1090)内取值的概率为99.7%,故灯泡的最低使用寿命应控制在910h以上 
[名师指引]正态总体在(μ-3σ,μ+3σ)以外的概率只有千分之三,这是一个很小的概率  这样我们在研究问题时可以集中在(μ-3σ,μ+3σ)中研究,而忽略其中很小的一部分,从而简化了正态正态中研究的问题
这样我们在研究问题时可以集中在(μ-3σ,μ+3σ)中研究,而忽略其中很小的一部分,从而简化了正态正态中研究的问题
[新题导练]
2.难点:利用正态分布曲线的特点及曲线所表示的意义解决简单问题.
1.重点:利用实际问题的直方图,了解正态分布曲线的特点及曲线所表示的意义
4.对于 ,取值小于x的概率
,取值小于x的概率 .
.
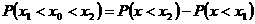

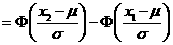 .
.
★ 重 难 点 突 破 ★
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com