
题目列表(包括答案和解析)
2.用逻辑联结词“且”把命题 和命题
和命题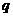 联结起来.就得到一个新命题,记作
联结起来.就得到一个新命题,记作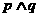 ,读作______
,读作______ 且
且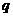 ____
____
1.“或”,“且”, “非”称为逻辑联结词___ , 不含逻辑联结词的命题称为简单命题_;
含有逻辑联结词的命题称为__复合命题______ ,复合命题有三种形式 且
且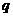 、
、 或
或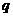 、非
、非
8.
|
 的概率分布列为
的概率分布列为
分别求出随机变量η= 2的分布列.
2的分布列.
|
 2对于
2对于 的不同取值-2,2及-1,1,η分别取相同的值4与1,即η取4这个值的概率为
的不同取值-2,2及-1,1,η分别取相同的值4与1,即η取4这个值的概率为 取-2与2值的概率
取-2与2值的概率 与
与 合并的结果,η取1这个值的概率为
合并的结果,η取1这个值的概率为 取-1与1值的概率
取-1与1值的概率 与
与 合并的结果,故η的分布列为
合并的结果,故η的分布列为
点评:在得到η的分布列中,η的取值行中无重复数,
概率行中各项必须非负,且各项之和一定等于1.
7. 某电视台的一个智力游戏节目中,有一道将四本由不同作者所著的外国名著A、B、C、D与它们的作者连线的题目,每本名著只能与一名作者连线,每名作者也只能与一本名著连线.每连对一个得3分,连错得 分,一名观众随意连线,他的得分记作ξ.
分,一名观众随意连线,他的得分记作ξ.
(1)求该观众得分ξ为非负的概率;
(2)求ξ的分布列及数学期望.
解: (1) 的可能取值为
的可能取值为 . ………………3分
. ………………3分

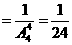 ,
,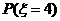
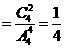 ,
,
 .……7分
.……7分
该同学得分非负的概率为
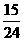 .…………8分
.…………8分
(2) 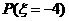
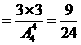 .………………10分
.………………10分
 的分布列为:
的分布列为:







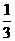


………………12分
数学期望 .………………14分
.………………14分
6.
5.
4.
3.
2.
1.甲、乙两人破译一种密码,它们能破译的概率分别为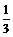 和
和 ,求:
,求:
(1)恰有一人能破译的概率;(2)至多有一人破译的概率;
(3)若要破译出的概率为不小于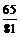 ,至少需要多少甲这样的人?
,至少需要多少甲这样的人?
(1)设A为“甲能译出”,B为“乙能译出”,则A、B互相独立,从而A与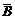 、
、 与B、
与B、 与
与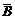 均相互独立.
均相互独立.
“恰有一人能译出”为事件 ,又
,又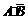 与
与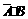 互斥,
互斥,
则
(2)“至多一人能译出”的事件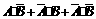 ,且
,且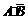 、
、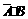 、
、 互斥,
互斥,
∴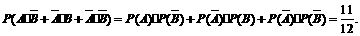
(3)设至少需要n个甲这样的人,而n个甲这样的人译不出的概率为 ,
,
∴n个甲这样的人能译出的概率为 ,
,
由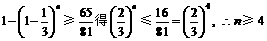
∴至少需4个甲这样的人才能满足题意.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com