
题目列表(包括答案和解析)
3.重难点:.
(1) 理解逻辑联结词 “非”的含义
问题1:你能写出下列命题p的非(否定)吗?
(1)p:100既能被4整除又能被5整除
(2)p:三条直线两两相交
(3)p:一元二次方程至多有两个解
(4)p:
解: (1) p:100不能被4整除,或不能被5整除
p:100不能被4整除,或不能被5整除
(2) p:三条直线不都两两相交
p:三条直线不都两两相交
(3) p:一元二次方程至少有三个解
p:一元二次方程至少有三个解
(4) p:
p: 或
或
点拨: “ 且
且 ”的否定形式是“
”的否定形式是“ 或
或 ”,而“
”,而“ 或
或 ”
”
的否定形式是“ 且
且 ”.
”.
写出命题的非(否定),需要对其正面叙述的词语进行否定,常用正面叙述词语及它的否定列举如下:
|
正面词语 |
且 |
小于(<) |
都是 |
都不是 |
至少n个 |
至多n个 |
|
否定词语 |
或 |
不小于(≥) |
不都是 |
至少有一个是 |
至多n-1个 |
至少n+1个 |
|
正面词语 |
任意的 |
所有的 |
有无穷多个 |
存在唯一的 |
对任意p,使…恒成立 |
|
否定词语 |
某个 |
某些 |
只有有限多个 |
不存在或至少存在两个 |
至少有一个p,使…不成立 |
(2)命题的否定与命题的否命题的区别
问题2: 写出命题:“若 ,则
,则 ”的否定与否命题,并加以区别。
”的否定与否命题,并加以区别。
解析:命题的否定:若 ,则
,则
命题的否命题:若 ,则
,则
点拨: 命题的否定,是对整个命题进行否定,侧重于对命题结论的否定.如具体到“若 则
则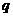 ”而言,命题的否定是只否定结论不否定条件.而命题的否命题则是既否定条件又否定结论.
”而言,命题的否定是只否定结论不否定条件.而命题的否命题则是既否定条件又否定结论.
(3)全称量词与存在量词
问题3:写出命题“若 ,则
,则 ”的否定
”的否定
解析:“若 ,则
,则 ”显然两个命题都是假命题,这就与复合命题中的真值表相矛盾.那么问题出在哪呢?实际上命题是省略了全称量词,命题里的“
”显然两个命题都是假命题,这就与复合命题中的真值表相矛盾.那么问题出在哪呢?实际上命题是省略了全称量词,命题里的“ ”是指“对于任意的
”是指“对于任意的 ”.所以原命题的否定形式就是:“存在
”.所以原命题的否定形式就是:“存在 ,使得
,使得 ”.这时原命题是假命题,而否定形式就是真命题.所以在判断复合命题的形式时,要准确理解命题的本质含义,尤其注意在一些表述中命题所隐含的全称量词.
”.这时原命题是假命题,而否定形式就是真命题.所以在判断复合命题的形式时,要准确理解命题的本质含义,尤其注意在一些表述中命题所隐含的全称量词.
点拨:全称量词有时会被省略。如:不少学生认为命题:“不等式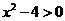 的解为
的解为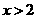 或
或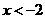 ”是“
”是“ 或
或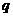 ”形式的复合命题:
”形式的复合命题:
 :不等式
:不等式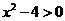 的解为
的解为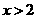
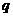 :不等式
:不等式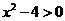 的解为
的解为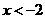
显然 假
假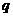 假,但“
假,但“ 或
或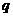 ”确为真,这与真值表相矛盾.实际上问题还是与上面的一样,命题里的“解”是指“所有的解”,这样“
”确为真,这与真值表相矛盾.实际上问题还是与上面的一样,命题里的“解”是指“所有的解”,这样“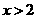 或
或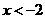 ”就是一个整体,所以上面的命题不是“
”就是一个整体,所以上面的命题不是“ 或
或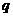 ”形式的复合命题,应该是个简单命题.
”形式的复合命题,应该是个简单命题.
★ 热 点 考 点 题 型 探 析★
考点一: 复合命题及其真假判断
题型1. 指出复合命题的形式及构成它的简单命题,反之能写出“p或q”“p且q”“非p”形式的复合命题
[例1] 分别指出下列复合命题的形式及构成它的简单命题:
(1)3是质数或合数.
(2)他是运动员兼教练员.
(3)相似三角形不一定是全等三角形.
[解题思路]:根据组成上述各复合命题的语句中所出现的逻辑联结词,“且”“或”“非”进行命题结构的判断.
解析: (1) 这个命题是“p或q”形式,其中p:3是质数,q:3是合数.
(2) 这个命题是“p且q”形式,其中p:他是运动员,q:他是教练员.
(3) 这个命题是“非p”形式,其中p:相似三角形一定是全等三角形..
[例2] 分别写出下列各组命题构成的“p或q”“p且q”“非p”形式的复合命题:
(1)p:连续的三个整数的乘积能被2整除, q:连续的三个整数的乘积能被3整除.
(2)p:对角线互相垂直的四边形是菱形, q:对角线互相平分的四边形是菱形.
[解题思路]:在由简单命题写出复合命题时,本例的(1)、(2)可直接使用逻辑联结记词,而(3)中的“p或q”“p且q”“非p”,写复合命题时,关键要搞清“且”“或”“非”的意义.
解析: (1)根据真值表,复合命题可以写成简单形式:
p或q:连续的三个整数的乘积能被2或能被3整除. p且q:连续的三个整数的乘积能被2且能被3整除. 非p:连续的三个整数的乘积不能被2整除. ∵连续的三整数中有一个(或两个)是偶数,而有一个是3的倍数,
(2)根据真值表,只能用逻辑联结词联结两个命题,不能写成简单形式:
p或q:对角线互相垂直的四边形是菱形或对角线互相平分的四边形是菱形.p且q:对角线互相垂直的四边形是菱形且对角线互相平分的四边形是菱形.非p:对角线互相垂直的四边形不一定是菱形.
[名师指引]要理解逻辑联结词“且”、“或”和 “非”的含义, “且”是指必须两个都选,“或”是指两个中至少选一个,“非”是指否定的意思,尤其要注意理解和掌握常见正面词语的否定词语.
[新题导练]
2.难点:对逻辑联结词“或”、“且”和“非”的含义的理解;写出全称命题与特称命题否定
1.重点:判断复合命题“p且q”、“p或q”、“非p”的真假;判断全称命题与特称命题真假
9.全称命题形式: ;特称命题形式:
;特称命题形式: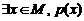 。 其中M为给定的集合,
。 其中M为给定的集合,
特别提醒:
全称命题p: 的否定
的否定 p:
p: ;全称命题的否定为特称命题
;全称命题的否定为特称命题
特称命题p: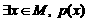 的否定
的否定 p:
p: ;特称命题的否定为全称命题
;特称命题的否定为全称命题
其中p(x)是一个关于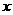 的命题。
的命题。
★ 重 难 点 突 破 ★
8.含有全称量词的命题称为全称命题__;含有存在量词的命题称为__特称命题__.
7.短语“存在一个”、“_至少有一个” 逻辑中称为存在量词,并用符号“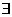 ” 表示。
” 表示。
6.短语“_对所有的”、“对任意一个” 逻辑中称为全称量词,并用符号“___ __” 表示。
__” 表示。
5.三种复合命题的真值表:
(1)“p且q”: 一假即假(2)“p或q”: 一真即真(3)“非p”: 真假相反
特别提醒: 命题的“否定”与“否命题”是不同的概念,对命题p的否定(即非p)是否定命题p所作的判断,而“否命题”是 “若 p则
p则  q ”
q ”
4. 对一个命题 的全盘否定, 就得到一个新的命题, 记作__
的全盘否定, 就得到一个新的命题, 记作__ p ___,读作___非
p ___,读作___非 _____
_____
3.用逻辑联结词“或”把命题 和命题
和命题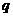 联结起来.就得到一个新命题,记作___
联结起来.就得到一个新命题,记作___ ____,读作___
____,读作___  或
或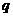 ______
______
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com