
题目列表(包括答案和解析)
5. 在数列 中,
中,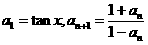 ,
,
(1)写出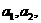
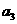 ;(2)求数列
;(2)求数列 的通项公式
的通项公式
[解析] 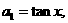
 ,
, ,猜想
,猜想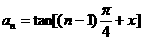
下面用数学归纳法证明:(1)当n=1时,由上面的探求可知猜想成立
(2)假设n=k时猜想成立,即
则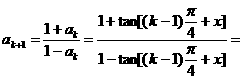

所以当n=k+1时,猜想也成立
综合(1)(2),对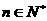 猜想都成立
猜想都成立
★抢分频道★
基础巩固训练
4.数列 中,
中,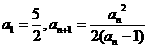
 ,用数学归纳法证明:
,用数学归纳法证明:
[解析](1) 当n=1时, 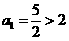 ,不等式成立
,不等式成立
(2)假设当n=k时等式成立,即 ,
,
则
 ,
,
 当n=k+1时, 不等式也成立
当n=k+1时, 不等式也成立
综合(1)(2),不等式对所有正整数都成立
题型2 用“归纳--猜想--证明”解决数学问题
[例3 ]是否存在常数a、b、c,使等式 对一切正整数n都成立?证明你的结论
对一切正整数n都成立?证明你的结论
[解题思路]从特殊入手,探求a、b、c的值,考虑到有3个未知数,先取n=1,2,3,列方程组求得,然后用数学归纳法对一切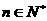 ,等式都成立
,等式都成立
[解析] 把n=1,2,3代入得方程组 ,解得
,解得 ,
,
猜想:等式 对一切
对一切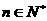 都成立
都成立
下面用数学归纳法证明:(1)当n=1时,由上面的探求可知等式成立
(2)假设n=k时等式成立,即 则
则
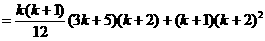


所以当n=k+1时,等式也成立
综合(1)(2),对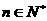 等式都成立
等式都成立
[名师指引]这是一个探索性命题,“归纳--猜想--证明”是一个完整的发现问题和解决问题的思维模式
[新题导练]
3. 用数学归纳法证明等式: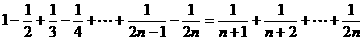
[解析] (1)当n=1时,左= =右,等式成立
=右,等式成立
(2)假设当n=k时等式成立,即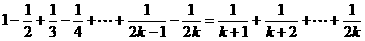
则
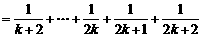
 当n=k+1时,等式也成立
当n=k+1时,等式也成立
综合(1)(2),等式对所有正整数都成立
2.用数学归纳法证明不等式 的过程中,由k推导到k+1时,不等式左边增加的式子是
的过程中,由k推导到k+1时,不等式左边增加的式子是
[解析]求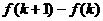 即可
即可
当 n=k时,左边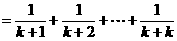 ,
,
n=k+1时,左边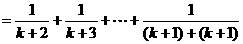 ,
,
故左边增加的式子是 ,即
,即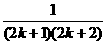
考点2 数学归纳法的应用
题型1:用数学归纳法证明数学命题(恒等式、不等式、整除性问题等)
[例2 ]用数学归纳法证明不等式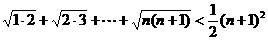
[解析](1)当n=1时,左=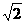 ,右=2,不等式成立
,右=2,不等式成立
(2)假设当n=k时等式成立,即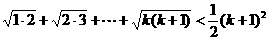
则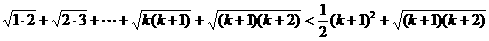


 当n=k+1时, 不等式也成立
当n=k+1时, 不等式也成立
综合(1)(2),等式对所有正整数都成立
[名师指引](1)数学归纳法证明命题,格式严谨,必须严格按步骤进行;
(2)归纳递推是证明的难点,应看准“目标”进行变形;
(3)由k推导到k+1时,有时可以“套”用其它证明方法,如:比较法、分析法等,表现出数学归纳法“灵活”的一面
[新题导练]
1.用数学归纳法证明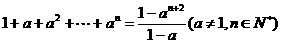 ,在验证n=1时,左边计算所得的式子是( )
,在验证n=1时,左边计算所得的式子是( )
A. 1
B. C.
C.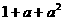 D.
D. 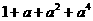
[解析] n=1时,左边的最高次数为1,即最后一项为 ,左边是
,左边是 ,故选B
,故选B
3.“归纳--猜想--证明”是一种重要的思维模式
问题3:在数列 中,
中, ,求数列
,求数列 的通项公式
的通项公式
点拨:本题有多种求法,“归纳--猜想--证明”是其中之一
解析: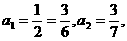
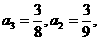 猜想
猜想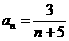
下面用数学归纳法证明:(1)当n=1时,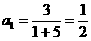 ,猜想成立
,猜想成立
(2)假设当n=k时猜想成立,则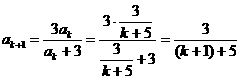
当n=k+1时猜想也成立
综合(1)(2),对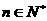 猜想都成立
猜想都成立
★热点考点题型探析★
考点1 数学归纳法
题型:对数学归纳法的两个步骤的认识
[例1 ] 已知n是正偶数,用数学归纳法证明时,若已假设n=k( 且为偶数)时命题为真,,则还需证明( )
且为偶数)时命题为真,,则还需证明( )
A.n=k+1时命题成立 B. n=k+2时命题成立
C. n=2k+2时命题成立 D. n=2(k+2)时命题成立
[解析] 因n是正偶数,故只需证等式对所有偶数都成立,因k的下一个偶数是k+2,故选B
[名师指引]用数学归纳法证明时,要注意观察几个方面:(1)n的范围以及递推的起点(2)观察首末两项的次数(或其它),确定n=k时命题的形式 (3)从
(3)从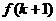 和
和 的差异,寻找由k到k+1递推中,左边要加(乘)上的式子
的差异,寻找由k到k+1递推中,左边要加(乘)上的式子
[新题导练]
2.归纳起点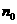 未必是1
未必是1
问题2:用数学归纳法证明:凸n边形的对角线条数为
点拔:本题的归纳起点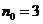
1.没有运用归纳假设的证明不是数学归纳法
问题1用数学归纳法证明:
错证:(1)当n=1时,左=右=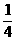 1,等式成立
1,等式成立
(2)假设当n=k时等式成立,
那么当n=k+1时,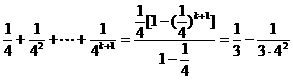
综合(1)(2),等式对所有正整数都成立
点拨:错误原因在于只有数学归纳法的形式,没有数学归纳法的“实质”即在归纳递推中,没有运用归纳假设
2.用数学归纳法可以证明许多与自然数有关的数学命题,其中包括恒等式、不等式、数列通项公式、整除性问题、几何问题等
★重难点突破★
重点:领会两个步骤的作用,运用数学归纳法证明一些简单的数学命题
难点:对不同类型的数学命题,完成从k到k+1的递推
重难点:了解数学归纳法的原理、正确运用数学归纳法
1.运用数学归纳法证明命题要分两步,第一步是归纳奠基(或递推基础),第二步是归纳递推(或归纳假设),两步缺一不可
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com