
题目列表(包括答案和解析)
15. 解:A={x|
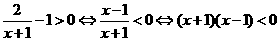 ∴ -1<x<1
∴ -1<x<1
∴A=(-1,1),定义域关于原点对称
f(-x)=lg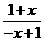 = lg
= lg =
= lg
lg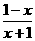 , ∴f(x)是奇函数.
, ∴f(x)是奇函数.
(2)B={x|

B=[-1-a,1-a]
当a ³2时, -1-a£-3, 1-a£-1,
由A=(-1,1),
B=[-1-a,1-a], 有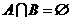
反之,若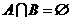 ,可取-a-1=2,则a=-3,a小于2. (注:反例不唯一)
,可取-a-1=2,则a=-3,a小于2. (注:反例不唯一)
所以,a ³2是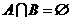 的充分非必要条件。
的充分非必要条件。
4.(广东省汕头市金山中学2009届高三期中考试(数学理))
函数 的定义域为集合
的定义域为集合 ,函数
,函数 的定义域为集合
的定义域为集合 . (1)判定函数
. (1)判定函数 的奇偶性,并说明理由.
的奇偶性,并说明理由.
(2)问: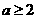 是
是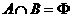 的什么条件(充分非必要条件 、必要非充分条件、充要条件、既非充分也非必要条件)? 并证明你的结论.
的什么条件(充分非必要条件 、必要非充分条件、充要条件、既非充分也非必要条件)? 并证明你的结论.
3.(广东省恩城中学2009届高三模拟)
已知命题p: ,命题q:
,命题q: ,则
,则 的_
_条件(填充分不必要条件、必要不充分条件、充要条件)。
的_
_条件(填充分不必要条件、必要不充分条件、充要条件)。
答案:充分不必要条件;
2.(广东省湛江市实验中学2009届高三月考(数学理))
“a+b>4且ab>4”是“a>2且b>2”的 ( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
答案:B
1.(广东省珠海市斗门第一中学2009届高三模拟)
 是
是 的 ( )
的 ( )
A. 充分不必要条件 B. 必要不充分条件
C. 充要条件 D. 既不充分也不必要条件
10.已知:a、b、c是互不相等的非零实数.
求证:三个方程ax2+2bx+c=0,bx2+2cx+a=0,cx2+2ax+b=0至少有一个方程有两个相异实根.
证明(反证法):假设三个方程中都没有两个相异实根,
则Δ1=4b2-4ac≤0,Δ2=4c2-4ab≤0,Δ3=4a2-4bc≤0.
相加有a2-2ab+b2+b2-2bc+c2+c2-2ac+a2≤0,
(a-b)2+(b-c)2+(c-a)2≤0. ①
由题意a、b、c互不相等,∴①式不能成立.
∴假设不成立,即三个方程中至少有一个方程有两个相异实根.
备用:
9. (2008学年中山市一中高三年测试题理科数学)
已知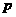 :
: ,
,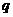 :
:
且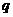 是
是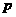 的必要不充分条件,求实数
的必要不充分条件,求实数 的取值范围。
的取值范围。
解:由
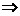

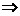
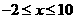 即
即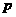 为:
为: …………………4分
…………………4分
而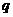 为:
为: , ………………………6分
, ………………………6分
又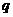 是
是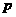 的必要不充分条件, 即
的必要不充分条件, 即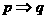
所以 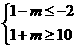
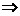
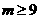
即实数 的取值范围为
的取值范围为 。
………………………12分
。
………………………12分
8.写出命题“乘积为奇数的两个整数都不是偶数”的逆命题、否命题、逆否命题,并判断真假.
解:典型错解: 原命题可写成:若两个整数的乘积为奇数,则它们都不是偶数, 是真命题.
逆命题:若两个整数的乘积都不是偶数,则这两个整数的乘积为奇数, 是真命题.
否命题:若两个整数的乘积不为奇数,则这两个整数不都是偶数, 是真命题.
逆否命题:若两个整数中不都是偶数,则这两个整数的乘积不为奇数, 是真命题.
否命题:若两个整数的乘积不为奇数,则这两个整数至少有一个是偶数;
点拨: 对“都不”的否定,许多同学都误认为是“不都”,这是错误的,应为“至少有一个”, 而“不都”是对“都”的否定.
正确解答: 原命题可写成:若两个整数的乘积为奇数,则它们都不是偶数, 是真命题.
逆命题:若两个整数的乘积都不是偶数,则这两个整数的乘积为奇数, 是真命题.
否命题:若两个整数的乘积不为奇数,则这两个整数至少有一个是偶数, 是真命题.
逆否命题:若两个整数中至少有一个是偶数,则这两个整数的乘积不为奇数, 是真命题.
7.用反证法证明:“已知x、y∈R,x+y≥2,求 证x、y中至少有一个大于1”. 则所作的反设是
答案: 假设x<1且y<1
6. (黄家中学高08级十二月月考)
条件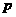 :
: ,条件
,条件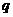 :
: 在
在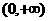 内是增函数,则
内是增函数,则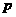 是
是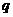 的
的
A.充要条件 B.充分不必要条件
C.必要不充分条件 D.既不充分也不必要条件
答案:∵ 在
在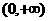 内是增函数
内是增函数
∴ ,
,
∴ ∴
∴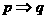 且
且 ∴
∴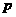 是
是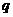 的充分不必要条件 故选B;
的充分不必要条件 故选B;
综合拔高训练
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com