
题目列表(包括答案和解析)
11.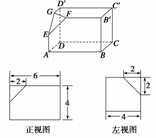 (2008·海南、宁夏文,18)如下的三个图中,上面的是一个长方体截去一个角所得多面体的直观图,它的正视图和左视图在下面画出(单位:cm).
(2008·海南、宁夏文,18)如下的三个图中,上面的是一个长方体截去一个角所得多面体的直观图,它的正视图和左视图在下面画出(单位:cm).
(1)在正视图下面,按照画三视图的要求画出该多面体的俯视图;
(2)按照给出的尺寸,求该多面体的体积;
(3)在所给直观图中连接BC′,证明:BC′∥平面EFG.
(1)解 如图(1)所示.
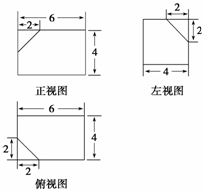
图(1)
(2)解 所求多面体体积
V=V长方体-V正三棱锥
=4×4×6- ×(
×(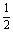 ×2×2)×2=
×2×2)×2=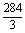 (cm3).
(cm3).
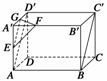 (3)证明 如图(2),在长方体ABCD-A′B′C′D′中,
(3)证明 如图(2),在长方体ABCD-A′B′C′D′中,
连接AD′,则AD′∥BC′.
因为E,G分别为AA′,A′D′的中点,
所以AD′∥EG,从而EG∥BC′.
又BC′ 平面EFG,
图(2)
平面EFG,
图(2)
所以BC′∥面EFG.
10.正方形ABCD与正方形ABEF所在平面相交于AB,在AE、BD上各有一点P、Q,且AP=DQ.
求证:PQ∥平面BCE.
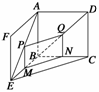 证明 方法一 如图所示,作PM∥AB交BE于M,作QN∥AB交BC于N,连接MN.
证明 方法一 如图所示,作PM∥AB交BE于M,作QN∥AB交BC于N,连接MN.
∵正方形ABCD和正方形ABEF有公共边AB,∴AE=BD.
又∵AP=DQ,∴PE=QB,
又∵PM∥AB∥QN,
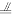 ∴
∴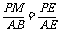 ,
,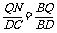 ,
,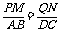 ,∴PM QN,
,∴PM QN,
∴四边形PMNQ为平行四边形,∴PQ∥MN.
又MN 平面BCE,PQ
平面BCE,PQ 平面BCE,
平面BCE,
∴PQ∥平面BCE.
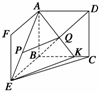 方法二 如图所示,连接AQ,并延长交BC于K,连接EK,
方法二 如图所示,连接AQ,并延长交BC于K,连接EK,
∵AE=BD,AP=DQ,∴PE=BQ,
∴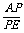 =
=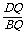 ①
①
又∵AD∥BK,∴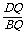 =
=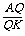 ②
②
由①②得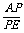 =
=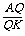 ,∴PQ∥EK.
,∴PQ∥EK.
又PQ 平面BCE,EK
平面BCE,EK 平面BCE,∴PQ∥平面BCE.
平面BCE,∴PQ∥平面BCE.
方法三 如图所示,在平面ABEF内,过点P作PM∥BE,交AB于点M,连接QM.
∵PM∥BE,PM 平面BCE, 即PM∥平面BCE,
平面BCE, 即PM∥平面BCE,
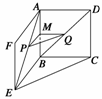 ∴
∴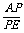 =
=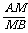 ①
①
又∵AP=DQ,∴PE=BQ,
∴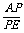 =
=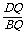 ②
②
由①②得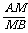 =
=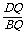 ,∴MQ∥AD,
,∴MQ∥AD,
∴MQ∥BC,又∵MQ 平面BCE,∴MQ∥平面BCE.
平面BCE,∴MQ∥平面BCE.
又∵PM∩MQ=M,∴平面PMQ∥平面BCE, PQ 平面PMQ,∴PQ∥平面BCE.
平面PMQ,∴PQ∥平面BCE.
9.如图所示,在正方体ABCD-A1B1C1D1中,O为底面ABCD的中心,P是DD1的中点,设Q是CC1上的点,问:当点Q在什么位置时,平面D1BQ∥平面PAO?
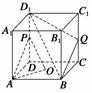 解 当Q为CC1的中点时,
解 当Q为CC1的中点时,
平面D1BQ∥平面PAO.
∵Q为CC1的中点,P为DD1的中点,∴QB∥PA.
∵P、O为DD1、DB的中点,∴D1B∥PO.
又PO∩PA=P,D1B∩QB=B,
D1B∥平面PAO,QB∥平面PAO,
∴平面D1BQ∥平面PAO.
8.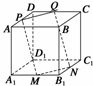 如图所示,ABCD-A1B1C1D1是棱长为a的正方体,M,N分别是下底面的棱A1B1,
如图所示,ABCD-A1B1C1D1是棱长为a的正方体,M,N分别是下底面的棱A1B1,
B1C1的中点,P是上底面的棱AD上的一点,AP=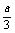 ,过P,M,N的平面交上
,过P,M,N的平面交上
底面于PQ,Q在CD上,则PQ= .
答案 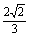 a
a
7.考察下列三个命题,在“
”处都缺少同一个条件,补上这个条件使其构成真命题(其中l,m为不同的直线, 、
、 为不重合的平面),则此条件为
.
为不重合的平面),则此条件为
.
|
|
|
|


|

|
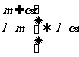 ②
②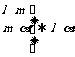 ③
③
答案 l

6.下列关于互不相同的直线m,l,n和平面 ,
, 的四个命题:
的四个命题:
①若m
 ,l∩
,l∩ =A,点A
=A,点A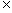 m,则l与m不共面;
m,则l与m不共面;
②若m,l是异面直线,l∥ ,m∥
,m∥ ,且n⊥l,n⊥m,则n⊥
,且n⊥l,n⊥m,则n⊥ ;
;
③若l∥ ,m∥
,m∥ ,
, ∥
∥ ,则l∥m;
,则l∥m;
④若l
 ,m
,m
 ,l∩m=A,l∥
,l∩m=A,l∥ ,m∥
,m∥ ,则
,则 ∥
∥ .
.
其中假命题的序号是 .
答案 ③
5.(2008·湖南理,5)设有直线m、n和平面 、
、 .下列命题不正确的是
(填序号).
.下列命题不正确的是
(填序号).
①若m∥ ,n∥
,n∥ ,则m∥n,②若m
,则m∥n,②若m
 ,n
,n
 ,m∥
,m∥ ,n∥
,n∥ ,则
,则 ∥
∥
③若 ⊥
⊥ ,m
,m
 ,则m⊥
,则m⊥ ,④若
,④若 ⊥
⊥ ,m⊥
,m⊥ ,m
,m
 ,则m∥
,则m∥
答案 ①②③
4.(2008·海南,宁夏文,12)已知平面 ⊥平面
⊥平面 ,
, ∩
∩ =l,点A∈
=l,点A∈ ,A
,A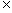 l,直线AB∥l,直线
l,直线AB∥l,直线
AC⊥l,直线m∥ ,m∥
,m∥ ,则下列四种位置关系中,一定成立的是 .
,则下列四种位置关系中,一定成立的是 .
①AB∥m ②AC⊥m ③AB∥ ④AC⊥
④AC⊥
答案 ①②③
3.对于不重合的两个平面 与
与 ,给定下列条件:
,给定下列条件:
①存在平面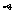 ,使得
,使得 ,
, 都垂直于
都垂直于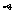 ;②存在平面
;②存在平面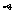 ,使得
,使得 ,
, 都平行于
都平行于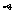 ;
;
③存在直线l
 ,直线m
,直线m
 ,使得l∥m;④存在异面直线l、m,使得l∥
,使得l∥m;④存在异面直线l、m,使得l∥ ,l∥
,l∥ ,m∥
,m∥ ,m∥
,m∥ .
.
其中,可以判定 与
与 平行的条件有
(写出符合题意的序号).
平行的条件有
(写出符合题意的序号).
答案 ②④
2.写出平面 ∥平面
∥平面 的一个充分条件
(写出一个你认为正确的即可).
的一个充分条件
(写出一个你认为正确的即可).
答案 存在两条异面直线a,b,a
 ,b
,b
 ,a∥
,a∥ ,b∥
,b∥
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com