11．(2010·淄博模拟)在平面直角坐标系xOy中，直线l与抛物线y²＝4x相交于不同的A、B两点．

(1)如果直线l过抛物线的焦点，求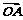·的值；

(2)如果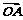·＝－4，证明直线l必过一定点，并求出该定点．

解：(1)由题意：抛物线焦点为(1,0)，

设l：x＝ty+1，代入抛物线y²＝4x，

消去x得y²－4ty－4＝0，

设A(x₁，y₁)，B(x₂，y₂)，

则y₁+y₂＝4t，y₁y₂＝－4，

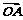∴·＝x₁x₂+y₁y₂＝(ty₁+1)(ty₂+1)+y₁y₂

＝t²y₁y₂+t(y₁+y₂)+1+y₁y₂

＝－4t²+4t²+1－4＝－3.

(2)设l：x＝ty+b代入抛物线y²＝4x，消去x得

y²－4ty－4b＝0，设A(x₁，y₁)，B(x₂，y₂)，

则y₁+y₂＝4t，y₁y₂＝－4b，

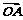∴·＝x₁x₂+y₁y₂＝(ty₁+b)(ty₂+b)+y₁y₂

＝t²y₁y₂+bt(y₁+y₂)+b²+y₁y₂

＝－4bt²+4bt²+b²－4b＝b²－4b.

令b²－4b＝－4，∴b²－4b+4＝0，∴b＝2，

∴直线l过定点(2,0)．

∴若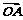·＝－4，则直线l必过一定点．

10．已知动圆过定点P(1,0)，且与定直线l：x＝－1相切，点C在l上．

(1)求动圆圆心的轨迹M的方程；

(2)设过点P，且斜率为－的直线与曲线M相交于A、B两点．

问△ABC能否为正三角形？若能，求出C点的坐标；若不能，说明理由．

解：(1)依题意，曲线M是以点P为焦点，直线l为准线的抛物

线，所以曲线M的方程为y²＝4x.如图所示．

　(2)由题意得，直线AB的方程为

y＝－(x－1)，

由

消y得

3x²－10x+3＝0.

解得A(，)，B(3，－2)．

若△ABC能为正三角形，

设C(－1，y)，则|AC|＝|AB|＝|BC|，即

①②组成的方程组无解，因此直线l上不存在点C使△ABC是正三角形．

9．(2011·南京调研)已知点M是抛物线y²＝4x上的一点，F为抛物线的焦点，A在圆C：(x－4)²+(y－1)²＝1上，则|MA|+|MF|的最小值为________．

解析：依题意得|MA|+|MF|≥(|MC|－1)+|MF|＝(|MC|+|MF|)－1，由抛物线的定义知|MF|等于点M到抛物线的准线x＝－1的距离，结合图形不难得知，|MC|+|MF|的最小值等于圆心C(4,1)到抛物线的准线x＝－1的距离，即为5，因此所求的最小值为4.

答案：4

8．若抛物线y²＝2px的焦点与双曲线－＝1的右焦点重合，则p的值为________．

解析：双曲线－＝1的右焦点F(3,0)是抛物线y²＝2px的焦点，所以＝3，p＝6.

答案：6

7．在平面直角坐标系xOy中，已知抛物线关于x轴对称，顶点在原点O，且过点P(2,4)，则该抛物线的方程是______________．

解析：由题意设抛物线的方程为y²＝2ax(a>0)，由于其过点P(2,4)，所以4²＝2a×2⇒a＝4，故该抛物线的方程是y²＝8x.

答案：y²＝8x

6．已知抛物线y²＝4x上两个动点B、C和点A(1,2)，且∠BAC＝90°，则动直线BC必过定点(　)

A．(2,5) 　　　　　　B．(－2,5)

C．(5，－2) 　　　　　D．(5,2)

解析：设B(，y₁)，C(，y₂)，BC的中点为D(x₀，y₀)，则y₁+y₂＝2y₀，直线BC：＝，即：4x－2y₀y+y₁y₂＝0　①；又·＝0，∴y₁y₂＝－4y₀－20，代入①式得：2(x－5)－y₀(y+2)＝0，则动直线BC恒过x－5＝0与y+2＝0的交点(5，－2)．

答案：C

5．(2011·济南第二次诊断)设斜率为2的直线l过抛物线y²＝ax(a≠0)的焦点F，且和y轴交于点A，若△OAF(O为坐标原点)的面积为4，则抛物线的方程为(　)

A．y²＝±4x 　　　　　　　B．y²＝±8x

C．y²＝4x　 　　　　　　　D．y²＝8x

解析：由题可知抛物线焦点坐标为(，0)，于是过焦点且斜率为2的直线的方程为y＝2(x－)，令x＝0，可得A点坐标为(0，－)，所以S_△OAF＝··＝4，∴a＝±8.

答案：B

4．已知过抛物线y²＝6x焦点的弦长为12，则此弦所在直线的倾斜角是(　)

A.或 　　　　　B.或

C.或 　　　　　 D.

解析：由焦点弦长公式|AB|＝得＝12，∴sinθ＝，∴θ＝或.

答案：B

3．过点(0,1)作直线，使它与抛物线y²＝4x仅有一个公共点，这样的直线有(　)

A．1条　 　　　　B．2条

C．3条　 　　　　D．4条

解析：结合图形分析可知，满足题意的直线共有3条：直线x＝0，过点(0,1)且平行于x轴的直线以及过点(0,1)且与抛物线相切的直线(非直线x＝0)．

答案：C

2．(2011·东北三校)抛物线y²＝8x的焦点到双曲线－＝1的渐近线的距离为(　)

A．1　 　　　　　　B.

C. 　　　　　　D.

解析：由题意可知，抛物线y²＝8x的焦点为(2,0)，双曲线－＝1的渐近线为y＝±x，所以焦点到双曲线的渐近线的距离为＝1.

答案：A