3.写出下列命题的否定并判断真假.　

(1)p：所有末位数字是0的整数都能被5整除；　

(2)q：x≥0，x²>0;　

(3)r：存在一个三角形，它的内角和大于180°;　

(4)t:某些梯形的对角线互相平分.　

回顾总结

知识:

方法：

思想：

2．已知a>0,设命题p：函数y=a^x在R上单调递减，q：不等式x+|x-2a|>1的解集为R，若p和q中有且只有一个命题为真命题，求a的取值范围.　

1.分别指出由下列命题构成的“pq”、“pq”、“p”形式的命题的真假.

(1)p：4∈{2，3}，q：2∈{2，3}；　

(2)p：1是奇数，q：1是质数；　

(3)p：0∈，q：{x|x²-3x-5<0}R；　

(4)p：5≤5，q：27不是质数；　

(5)p：不等式x²+2x-8<0的解集是{x|-4<x<2},q：不等式x²+2x-8<0的解集是{x|x<-4或x>2}.　

5.命题：“至少有一个点在函数y=kx (k≠0)的图象上”的否定是　　　　　 .　　　　　　　　　　　　　　　　　 　　　　　　　　　　

例题精讲

例1分别指出由下列命题构成的“pq”、“pq”、“p”形式的命题的真假.

(1)p:3是9的约数,q:3是18的约数;　

(2)p:菱形的对角线相等,q:菱形的对角线互相垂直;　

(3)p:方程x²+x-1=0的两实根符号相同,　

q:方程x²+x-1=0的两实根绝对值相等.　

(4)p:是有理数,q: 是无理数.　

例2　 已知两个命题r(x):sinx+cosx>m,s(x):x²+mx+1>0.如果对x∈R,r(x)与s(x)有且仅有一个是真命题.求实数m的取值范围.

　例3 写出下列命题的“否定”，并判断其真假.　

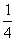(1)p：x∈R，x²-x+≥0；　

(2)q：所有的正方形都是矩形；　

(3)r：x∈R，x²+2x+2≤0；　

(4)s：至少有一个实数x，使x³+1=0.　

巩固练习

4.下列命题中不是全称命题的是　　　　　 (填序号).

　 ①圆有内接四边形　　　　　　　 ② >　　　　　　 ?　 ③≤

　④若三角形的三边长分别为3,4,5，则这个三角形为直角三角形　

3.已知命题p：所有有理数都是实数；命题q：正数的对数都是负数，则下列命题中为真命题

的是　　　　 (填序号).

　①( )　　　　 　　　②pq　　　　 　　③ ( ) (　　　 ④( )

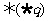
2.已知命题p:3≥3;q:3＞4，则下列判断不正确的是　　　　 (填序号).

①pq为假，pq为假, p为真　　　　　　　　 ②pq为真，pq为假，p为真

③pq为假，pq为假，p为假　　　　　　　　 ④ pq为真，pq为假，p为假

1.已知命题p:则为　　　　　 .　　　　　　　　　　　　　　　　　　　　　

12．(2010·山东烟台)已知直线l₁：2x－y+a＝0(a>0)，直线l₂：－4x+2y+1＝0和直线l₃：x+y－1＝0，且l₁与l₂的距离是.

(1)求a的值；

(2)能否找到一点P，使得P点同时满足下列三个条件：①P是第一象限的点；②P点到l₁的距离是P点到l₂的距离的；③P点到l₁的距离与P点到l₃的距离之比是∶；若能，求P点坐标；若不能，说明理由．

解：(1)直线l₂：2x－y－＝0.

所以l₁与l₂的距离d＝＝，

所以＝

所以|a+|＝.

因为a>0，所以a＝3.

(2)假设存在点P，设点P(x₀，y₀)，若P点满足条件②，则P点在与l₁、l₂平行的直线l′：2x－y+C＝0上，

且＝，即C＝，或C＝，

所以2x₀－y₀+＝0，或2x₀－y₀+＝0；

若P点满足条件③，由点到直线的距离公式，

有＝，

即|2x₀－y₀+3|＝|x₀+y₀－1|，

所以x₀－2y₀+4＝0或3x₀+2＝0；

由于P在第一象限，所以3x₀+2＝0不可能．

联立方程2x₀－y₀+＝0和x₀－2y₀+4＝0，

解得应舍去．

由解得

∴存在点P(，)同时满足三个条件．

11．已知直线l：3x－y+3＝0，求：

(1)点P(4,5)关于l的对称点；

(2)直线x－y－2＝0关于直线l对称的直线方程．

解：设P(x，y)关于直线l：3x－y+3＝0的对称点为P′(x′，y′)．

∵k_PP′·k_l＝－1，即×3＝－1.①

又PP′的中点在直线3x－y+3＝0上，

∴3×－+3＝0.②

由①②得

(1)把x＝4，y＝5代入③及④得x′＝－2，y′＝7，

∴P(4,5)关于直线l的对称点P′的坐标为(－2,7)．

(2)用③④分别代换x－y－2＝0中的x，y，得关于l的对称直线方程为－－2＝0，化简得7x+y+22＝0.