
题目列表(包括答案和解析)
9.已知集合A={x|mx2-2x+3=0,m∈R}.
(1)若A是空集,求m的取值范围;
(2)若A中只有一个元素,求m的值;
(3)若A中至多只有一个元素,求m的取值范围.
解 集合A是方程mx2-2x+3=0在实数范围内的解集.
(1)∵A是空集,∴方程mx2-2x+3=0无解.∴Δ=4-12m<0,即m> .
.
(2)∵A中只有一个元素,∴方程mx2-2x+3=0只有一个解.
若m=0,方程为-2x+3=0,只有一解x= ;若m≠0,则Δ=0,即4-12m=0,m=
;若m≠0,则Δ=0,即4-12m=0,m= .
.
∴m=0或m= .
.
(3)A中至多只有一个元素包含A中只有一个元素和A是空集两种含义,根据(1)、(2)的结果,得m=0或m≥ .
.
8.(2008·福建理,16) 设P是一个数集,且至少含有两个数,若对任意a、b∈P,都有a+b、a-b、ab、 ∈P(除数b≠0),则称P是一个数域.例如有理数集Q是数域;数集F={a+b
∈P(除数b≠0),则称P是一个数域.例如有理数集Q是数域;数集F={a+b |a,b∈Q}也是数域.有下列命题:
|a,b∈Q}也是数域.有下列命题:
①整数集是数域;
②若有理数集Q M,则数集M必为数域;
M,则数集M必为数域;
③数域必为无限集;
④存在无穷多个数域.
其中正确的命题的序号是 .(把你认为正确的命题的序号都填上)
答案 ③④
7.集合A={x||x-3|<a,a>0},B={x|x2-3x+2<0},且B A,则实数a的取值范围是 .
A,则实数a的取值范围是 .
答案 [2,+∞)
6.(2009·徐州模拟)设A,B是非空集合,定义A×B= ,已知A=
,已知A= ,
,
B= ,则A×B=
.
,则A×B=
.
答案

4.集合A={y∈R|y=lgx,x>1},B={-2,-1,1,2},则( RA)∩B=
.
RA)∩B=
.
答案 {-2,-1}
5已知集合P={(x,y)||x|+|y|=1},Q={(x,y)|x2+y2≤1},则P与Q的关系为 .
答案 P Q
Q
3.设全集U=R,集合M={x|x≤1或x≥3},集合P= ,且
,且 UM
UM ≠
≠ ,则实数k的取值
,则实数k的取值
范围是 .
答案 0<k<3
2.已知集合U={0,1,3,5,7,9},A∩ UB={1},B={3,5,7},那么(
UB={1},B={3,5,7},那么( UA)∩(
UA)∩( UB)=
.
UB)=
.
答案 {0,9}
1.(2008·江西理,2)定义集合运算:A*B=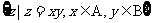 设A=
设A= B
B 则集合A*B
则集合A*B
的所有元素之和为 .
答案 6
20.(16分)设p:实数x满足x2-4ax+3a2<0,其中a<0;q:实数x满足x2-x-6≤0,或x2+2x-8>0,且 的必
的必
不充分条件,求a的取值范围.
解 设A={x|p}={x|x2-4ax+3a2<0,a<0}={x|3a<x<a,a<0},
B={x|q}={x|x2-x-6≤0或x2+2x-8>0}={x|x2-x-6≤0}∪{x|x2+2x-8>0}
={x|-2≤x≤3}∪{x|x<-4或x>2}=
∵ 的必要不充分条件,∴
的必要不充分条件,∴
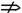
 .
.
则

 而
而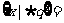
 RB=
RB=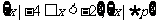 =
= RA=
RA=
∴


则 综上可得-
综上可得-
19.(16分)记函数f(x)= 的定义域为A,g(x)=lg
的定义域为A,g(x)=lg 的定义域为B.
的定义域为B.
(1)求A;
(2)若B A,求实数a的取值范围.
A,求实数a的取值范围.
解 (1)由2- 得
得 ∴x<-1或x≥1,即A=(-∞,-1)
∴x<-1或x≥1,即A=(-∞,-1)
 .
.
(2)由(x-a-1)(2a-x) >0,得(x-a-1)(x-2a)<0.∵a<1,∴a+1>2a,∵B=(2a,a+1).
又∵B A,∴2a≥1或a+1≤-1,即a≥
A,∴2a≥1或a+1≤-1,即a≥ 或a≤-2.∵a<1,∴
或a≤-2.∵a<1,∴ ≤a<1或a≤-2,
≤a<1或a≤-2,
故B A时,a的取值范围是
A时,a的取值范围是
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com