6.一个正三棱锥的四个顶点都在半径为1的球面上，其中底面的三个顶点在该球的一个大圆上，则该正三棱锥的体积是　　　　　 .

5.已知各顶点都在一个球面上的正四棱柱高为4，体积为16，则这个球的表面积是　　　　 .

4.若一个底面边长为，侧棱长为的正六棱柱的所有顶点都在一个球的面上，则此球的体积为　　　 .

3.已知三棱锥S-ABC的各顶点都在一个半径为r的球面上，球心O在AB上，SO⊥底面ABC，AC=r，则球的体积与三棱锥体积的比值是　　　　　　 .

2.长方体的过一个顶点的三条棱长的比是1∶2∶3，对角线长为2，则这个长方体的体积是　　　　 .

1. 如图所示，E、F分别是边长为1的正方形ABCD边BC、CD的中点，沿线AF，AE，EF折起来，则所围成的三棱锥的体积为　　　　 .

3.如图所示，在四棱锥P-ABCD中，底面ABCD为矩形，侧棱PA⊥底面ABCD，

AB=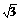， BC=1，PA=2，E为PD的中点.

(1)求直线AC与PB所成角的余弦值；

(2)在侧面PAB内找一点N，使NE⊥平面PAC，并求出N点到AB和AP的距离.

回顾总结

知识

方法

思想

2.已知：正四棱柱ABCD-A₁B₁C₁D₁中，底面边长为2，侧棱长为4， E、F分别为棱AB、BC

的中点.

(1)求证：平面B₁EF⊥平面BDD₁B₁；(2)求点D₁到平面B₁EF的距离.

1.如图所示，AF、DE分别是⊙O、⊙O₁的直径，AD与两圆所在的平面均垂直，AD=8.BC是⊙O的直径，AB=AC=6， OE∥AD.

(1)求二面角B-AD-F的大小；(2)求直线BD与EF所成的角的余弦值.

5.如图所示，在长方体ABCD-A₁B₁C₁D₁中，AB=BC=2，

AA₁=1，则BC₁与平面BB₁D₁D所成角的正弦值为　　　　 　.

例题精讲

例1.如图所示，已知点P在正方体ABCD-A′B′C′D′的对角线BD′上,∠PDA=60°.

(1)求DP与CC′所成角的大小; (2)求DP与平面AA′D′D所成角的大小.

例2.在三棱锥S-ABC中，△ABC是边长为4的正三角形，平面SAC⊥平面ABC， SA=SC=2，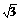

M、N分别为AB、SB的中点，如图所示.求点B到平面CMN的距离.

例3　 如图所示，四棱锥P-ABCD中，底面ABCD是矩形，PA⊥底面ABCD， PA=AB=1，AD=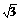

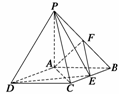点F是PB的中点，点E在边BC上移动.

(1)点E为BC的中点时，试判断EF与平面PAC的位置关系，并说明理由；

(2)求证：无论点E在BC边的何处，都有PE⊥AF；

(3)当BE为何值时，PA与平面PDE所成角的大小为45°.

巩固练习