2.下列条件中，不能判断两个平面平行的是　　　　 (填序号).

①一个平面内的一条直线平行于另一个平面，②一个平面内的两条直线平行于另一个平面

③一个平面内有无数条直线平行于另一个平面，④一个平面内任何一条直线都平行于另一个平面

1.下列命题中，正确命题的个数是　　　　　 .

①若直线l上有无数个点不在平面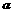内，则l∥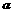;②若直线l与平面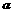平行，则l与平面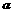内的任意一条直线都平行；③如果两条平行直线中的一条直线与一个平面平行，那么另一条直线也与这个平面平行；④若直线l与平面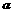平行，则l与平面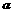内的任意一条直线都没有公共点.

3.如图所示，等腰直角三角形ABC中，∠A=90°，BC=，DA⊥AC，DA⊥AB，若DA=1，且E为DA的中点.求异面直线BE与CD所成角的余弦值.

回顾总结

知识

方法

思想

2.在正方体ABCD-A₁B₁C₁D₁中，E是CD的中点，连接AE并延长与BC的延长线交于点F，连接BE并延长交AD的延长线于点G，连接FG.

求证：直线FG平面ABCD且直线FG∥直线A₁B₁.

1.如图，E、F、G、H分别是空间四边形AB、BC、CD、DA上的点，且EH与FG相交于点O.

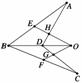求证：B、D、O三点共线.

5.如图所示，在正三角形ABC中，D、E、F分别为各边的中点，G、H、I、J分别为AF、AD、BE、DE的中点，将△ABC沿DE、EF、DF折成三棱锥以后，GH与IJ所成角的度数为　　　　　　 .

例题精讲

例1 如图所示，空间四边形ABCD中，E、F、G分别在AB、BC、CD上，且满足AE∶EB=CF∶FB

=2∶1，CG∶GD=　 3∶1，过E、F、G的平面交AD于H，连接EH.

(1)求AH∶HD；(2)求证：EH、FG、BD三线共点.

例2　 如图所示，正方体ABCD-A₁B₁C₁D₁中，M、N分别是A₁B₁，B₁C₁的中点.问：

(1)AM和CN是否是异面直线？说明理由；

(2)D₁B和CC₁是否是异面直线？说明理由.

例3　 如图所示，在四棱锥P-ABCD中，底面是边长为2的菱形，∠DAB=60°，对角线AC与BD交于点O，PO⊥平面ABCD，PB与平面ABCD所成角为60°.

(1)求四棱锥的体积；

(2)若E是PB的中点，求异面直线DE与PA所成角的余弦值.

巩固练习

4.如果一个凸多面体是n棱锥，那么这个凸多面体的所有顶点所确定的直线共有　　　 条.这些直线中共有f(n)对异面直线，则f(4)=　　　　　　 ;f(n)=　　　　　　 .(答案用数字或n的解析式表示)

3.若三个平面两两相交，且三条交线互相平行，则这三个平面把空间分成　　　　　 部分.

2.对于平面和直线l，内至少有一条直线与直线l　　　　　 (用“垂直”，“平行”或“异面”填空).

1.给出下列四个命题：

①垂直于同一直线的两条直线互相平行；

②垂直于同一平面的两个平面互相平行；

③若直线l₁、l₂与同一平面所成的角相等，则l₁,l₂互相平行；

④若直线l₁、l₂是异面直线，则与l₁、l₂都相交的两条直线是异面直线.

其中假命题的个数是　　　　 .