12.(1)是否存在实数p，使“4x+p<0”是“x²-x-2>0”的充分条件？如果存在，求出p的取值范围；　

(2)是否存在实数p,使“4x+p<0”是“x²-x-2>0”的必要条件？如果存在，求出p的取值范围.　

解 (1)当x>2或x<-1时,x²-x-2>0,　由4x+p<0,得x<-,故-≤-1时，　

“x<-”“x<-1”“x²-x-2>0”.　∴p≥4时，“4x+p<0”是“x²-x-2>0”的充分条件.　

(2)不存在实数p满足题设要求.

11.已知命题p：方程x²+mx+1=0有两个不等的负实数根；命题q:方程4x²+4(m-2)x+1=0无实数根.若“p或q”为真命题，“p且q”为假命题，求m的取值范围.　

解 　由p得：则m>2.　

由q知：Δ′=16(m-2)²-16=16(m²-4m+3)<0,则1<m<3.　

∵“p或q”为真，“p且q”为假，∴p为真，q为假，或p为假，q为真.　

则解得m≥3或1<m≤2.

10.写出下列命题的否命题及命题的否定形式,并判断真假:　

(1)若m>0,则关于x的方程x²+x-m=0有实数根;　

(2)若x、y都是奇数，则x+y是奇数；　

(3)若abc=0，则a、b、c中至少有一个为零.　

解 (1)否命题：若m≤0，则关于x的方程x²+x-m=0无实数根；(假命题)　

命题的否定：若m>0，则关于x的方程x²+x-m=0无实数根；(假命题)　

(2)否命题：若x、y不都是奇数，则x+y不是奇数；(假命题)　

命题的否定：若x、y都是奇数，则x+y不是奇数；(真命题)　

(3)否命题：若abc≠0,则a、b、c全不为0；(真命题)　

命题的否定：若abc=0，则a、b、c全不为0.(假命题)

9.指出下列命题的真假：　

(1)命题“不等式(x+2)²≤0没有实数解”；　

(2)命题“1是偶数或奇数”；　

(3)命题“属于集合Q，也属于集合R”；

(4)命题“AAB”.

解 　(1) 此命题为“p”的形式,其中p:“不等式(x+2)²≤0有实数解”，因为x=-2是该不等式的一个解，

所以p是真命题，即p是假命题，所以原命题是假命题.　

(2)此命题是“p∨q”的形式，其中p:“1是偶数”，q:“1是奇数”，因为p为假命题，q为真命题，　

所以p∨q是真命题，故原命题是真命题.　

(3)此命题是“p∧q”的形式，其中p:“属于集合Q”，q:“属于集合R”，因为p为假命题,q为真命题，所以p∧q是假命题，故原命题是假命题.

(4)此命题是“p”的形式，其中p:“因为p为真命题，

所以“p”为假命题，故原命题是假命题.

8.令p(x):ax²+2x+1>0,若对R，p(x)是真命题，则实数a的取值范围是　　　　　 .

答案　 a>1

7.(2009·姜堰中学高三综合卷)已知命题P:“R,x²+2x-3≥0”,请写出命题P的否定：　　　　　　　 .

　 答案　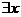 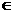R，x²+2x-3<02^{222　　 22222222222}　

6.若p、q是两个简单命题，且“p∨q”的否定是真命题，则必有p　　　 ，q 　　　　　.(用“真”、“假”填空).

　 答案　 假　　 假

5.若命题p:，则是

答案　 　xA或xB　

4.命题“存在x∈Z使2x²+x+m≤0”的否定是　　　　　　　　　　　　　　　　　　　 .

答案　 对任意x∈Z都有2x²+x+m>0

3.“p∨q”为真命题”是“p∧q为真命题”的　　　　　 条件.

　 答案　 必要不充分