8．某工厂生产某种产品固定成本为2 000万元，并且每生产一单位产品，成本增加10万元．又知总收入K是单位产品数Q的函数，K(Q)＝40Q－Q²，则总利润L(Q)的最大值是__________．

解析：总利润L(Q)＝40Q－Q²－10Q－2 000

＝－(Q－300)²+2 500.

故当Q＝300时，总利润最大值为2 500万元．

答案：2 500万元

7．某超市销售一种世博会纪念品，每件售价11.7元，后来，此纪念品的进价降低了6.4%，售价不变，从而超市销售这种纪念品的利润提高了8%.则这种纪念品的原进价是________元．

解析：设原进价为x元，则依题意有(11.7－x)(1+8%)＝11.7－(1－6.4%)x，解得x＝6.5.

答案：6.5

6.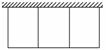有一批材料可以围成200米长的围墙，现用此材料在一边靠墙的地方围成一块矩形场地，且内部用此材料隔成三个面积相等的矩形(如图所示)，则围成的矩形场地的最大面积为(　)

A．1000米²　 　　　　　　　　　　　　　　　　 B．2000米²

C．2500米²　 　　　　　　　　　　　　　　　　 D．3000米²

解析：设三个面积相等的矩形的长、宽分别为x米、y米，如图所示．则4x+3y＝200，又S＝3xy＝3x·＝x(200－4x)＝－4(x－25)²+2500，

∴当x＝25时，S_max＝2500.

答案：C

5．拟定从甲地到乙地通话m分钟的电话费由f(m)＝1.06(0.5×[m]+1)给出，其中m>0，[m]是大于或等于m的最小整数(如[3]＝3，[3.7]＝4，[3.1]＝4)，则从甲地到乙地通话时间为5.5分钟的话费为(　)

A．3.71元　 　　　　　　　　　　　　　　 B．3.97元

C．4.24元 　　　　　　　　　　　 　　D．4.77元

解析：[5.5]＝6，f(5.5)＝1.06(0.5×6+1)＝4.24元．

答案：C

4．某产品的总成本y(万元)与产量x(台)之间的函数关系式为y＝3000+20x－0.1x²，x∈(0,240)，若每台售价25万元，则生产者不亏本的最低产量是(　)

A．100台　 　　　　　　　　　　　　　　　 B．120台

C．150台　 　　　　　　　　　　　　　　　 D．180台

解析：当总收入不低于总成本时生产者不亏本．

则25x≥3000+20x－0.1x²，

即：x²+50x－30000≥0.

解得x≥150或x≤－200(舍去)，

故最低产量为150台．

答案：C

3.某厂有许多形状为直角梯形的铁皮边角料(如图)，为降低消耗，开源节流，现要从这些边角料上截取矩形铁片(如图阴影部分)备用，当截取的矩形面积最大时，矩形两边的长x、y应为(　)

A．x＝15，y＝12　 　　　　　　　　　　　　　　　　 B．x＝12，y＝15

C．x＝14，y＝10　 　　　　　　　　　　　　　　　　 D．x＝10，y＝14

解析：依题意知：＝，即x＝(24－y)，

∴阴影部分的面积

S＝xy＝(24－y)y＝(－y²+24y)，

∴当y＝12时，S有最大值．

此时x＝15.

答案：A

2．某地2000年底人口为500万，人均住房面积为6 m²，如果该城市人口平均每年增长率为1%.问为使2010年底该城市人均住房面积增加到7 m²，平均每年新增住房面积至少为________万 m².(1.01¹⁰≈1.1045)(　)

A．90　 　　　　　　　　　　　　　　 　B．87

C．85 　　　　　　　　　　　　　　　 　D．80

解析：到2010年底该城市人口有500×(1+1%)¹⁰≈552.25万人，则≈86.6(万 m²)．

答案：B

1．某电视新产品投放市场后第一个月销售100台，第二个月销售200台，第三个月销售400台，第四个月销售790台，则下列函数模型中能较好地反映销量y与投放市场的月数x之间关系的是(　)

A．y＝100x　 　　　　　　　　　　　　　 B．y＝50x²－50x+100

C．y＝50×2^x　 　　　　　　　　　　　　 D．y＝100log₂x+100

解析：根据函数模型的增长差异和题目中的数据，应为指数型函数模型．

答案：C

12.已知在直三棱柱ABC-A₁B₁C₁中，AC⊥BC，D为AB的中点，AC=BC=BB₁.

求证：(1)BC₁⊥AB₁；(2)BC₁∥平面CA₁D.

11.在正方体ABCD-A₁B₁C₁D₁中，E、F分别是BB₁、CD的中点.

(1)求证：平面AED⊥平面A₁FD₁；

(2)在AE上求一点M，使得A₁M⊥平面ADE.