6．已知函数f(x)＝，若方程f(x)＝x+a有且只有两个不相等的实数根，则实数a的取值范围为(　)

A．(－∞，0]　 　　　　　　　　　　　　 B．[0,1)

C．(－∞，1)　 　　　　　　　　　　　　 D．[0，+∞)

解析：当x>0时，因为f(x)＝f(x－1)，所以当x>0时，f(x)是以1为周期的函数，又当0<x≤1时，x－1≤0，所以f(x)＝f(x－1)＝2^1－x－1＝2·()^x－1.方程f(x)＝x+a的根的个数可看成是两个函数y＝f(x)与y＝x+a的图象的交点个数，画出函数的图象，如图，由图象可知，实数a的取值范围是(－∞，1)．

答案：C

5．(2011·重庆模拟)若指数函数f(x)＝a^x(a>0，a≠1)图象上的任意一点P(x₀，y₀)处的导数都大于零，则函数y＝的图象的大致形状是(　)

解析：由题可知f(x)＝a^x是单调递增函数，所以a>1，又因为y＝＝，画图知其图象的大致形状为C.

答案：C

4．在同一坐标系中画出函数y＝log_ax，y＝a^x，y＝x+a的图象，可能正确的是(　)

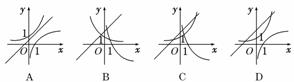
解析：当a>1时，y＝a^x，y＝log_ax和y＝x+a均为增函数，且y＝x+a在y轴的截距大于1，当0<a<1时，y＝a^x，y＝log_ax均为减函数，y＝x+a为增函数，且在y轴的截距在(0,1)内，结合图象可知选D.

答案：D

3．点P是球O的直径AB上的动点，PA＝x，过点P且与AB垂直的截面面积记为y，则y＝f(x)的大致图象是(　)

解析：先从起始点排除B，D选项，再用验证法，当点P为OA的中点时，截面面积大于大圆面积的一半，即可判定A正确．

答案：A

2．若函数y＝是奇函数，当x>0时，其对应的图象如图，则f(x)＝(　)

A．－2x－3　 　　　　　　 B．－2x+3

C．2x－3 　　　　　　　　　 D．2x+3

解析：显然点(，0)在y轴右侧的函数图象上，所以点(－，0)在y轴左侧的函数图象上，排除B、C，又由题设知函数为增函数，故选D.

答案：D

1．函数y＝x+cosx的大致图象是(　)

解析：当x＝0时，y＝1；当x＝时，y＝；当x＝－时，y＝－，观察各选项可知B正确．

答案：B

12．(文)诺贝尔奖发放方式为：每年一次，把奖金总金额平均分成6份，奖励在6项(物理、化学、文学、经济学、生理学和医学、和平)为人类做出了最有益贡献的人，每年发放奖金的总金额是基金在该年度所获利息的一半，另外一半利息用来增加基金总额，以便保证奖金数逐年增加，假设基金平均年利率为r＝6.24%.资料显示：1999年诺贝尔奖发奖后基金总额约为19800万美元，设f(x)表示为第x(x∈N^*)年诺贝尔奖发奖后的基金总额(1999年记为f(1))．

(1)用f(1)表示f(2)与f(3)，并根据所求结果归纳出函数f(x)的表达式．

(2)试根据f(x)的表达式判断网上一则新闻“2009年度诺贝尔奖各项奖金高达150万美元”是否为真，说明理由．

(参考数据：1.0624¹⁰≈1.83,1.0312¹⁰≈1.36,1.0624⁹≈1.72，1.0312⁹≈1.32)

解：(1)由题意知：

f(2)＝f(1)·(1+6.24%)－·f(1)·6.24%

＝f(1)·(1+3.12%)，

f(3)＝f(2)·(1+6.24%)－·f(2)·6.24%

＝f(2)(1+3.12%)＝f(1)·(1+3.12%)²，

∴f(x)＝19800·(1+3.12%)^x－1(x∈N^*)．

(2)2008年诺贝尔奖发放后基金总额为：

f(10)＝19800·(1+3.12%)⁹≈26100，

2009年度诺贝尔奖各项奖金额为××f(10)×6.24%≈136(万美元)，与150万美元相比少了约14万美元．

故新闻“2009年度诺贝尔奖各项奖金高达150万美元”是假新闻．

(理)上海某商店经销一种世博会纪念品，每件产品的成本为30元，并且每卖出一件产品需向税务部门缴税a元(a为常数，2≤a≤5)．根据市场调查，每件产品的日售价x(35≤x≤41)元与日销售量P(x)件的关系如下表所示：

现有日销售量P(x)的三种模拟函数：

①P(x)＝ke^x；②P(x)＝；③P(x)＝ke^30+x.

(1)求准确研究日销售量情况，应选择哪种模拟函数，为什么？

(2)求该商品的日利润L(x)元与每件产品的日售价x元的函数关系式；

(3)当每件产品的日销售价为多少元时，该商店的日利润L(x)最大．并求出L(x)的最大值．

解：(1)为准确研究日销售量情况，应选择模拟函数②.这是因为：将表格的数据分别代入三种模拟函数，

可判断这些点都满足关系式P(x)＝，

所以应选择模拟函数②，并且日销售量P(x)＝件．

(2)由(1)知，日销售量P(x)＝件．

则日利润L(x)＝(x－30－a)＝10e⁴⁰·(35≤x≤41)．

(3)由(2)知L′(x)＝10e⁴⁰·，

①当2≤a≤4时，33≤a+31≤35，

当35<x≤41时，L′(x)<0；

∴当x＝35时，L(x)取最大值，最大值为10(5－a)e⁵；

②当4<a≤5时，35<a+31≤36，令L′(x)＝0，得x＝a+31，

x，L′(x)，L(x)的变化情况如下表：

∴当x＝a+31时，L(x)取最大值10e^9－a.

综上所述，当2≤a≤4时，每件产品的日售价为35元时，该商店的日利润L(x)的最大值为10(5－a)e⁵元；

当4<a≤5时，每件产品的日售价为(a+31)元时，该商店的日利润L(x)的最大值为10e^9－a元．

11．经市场调查，某超市的一种小商品在过去近20天内的日销售量(件)与价格(元)均为时间t(天)的函数，且日销售量(件)近似满足g(t)＝80－2t，价格(元)近似满足f(t)＝20－|t－10|.

(1)试写出该种商品的日销售额y与时间t(0≤t≤20)的函数表达式；

(2)求该种商品的日销售额y的最大值与最小值．

解：(1)y＝g(t)·f(t)

＝(80－2t)·(20－|t－10|)

＝(40－t)(40－|t－10|)

＝.

(2)当0≤t<10时，y的取值范围是[1200,1225]，当t＝5时，y取得最大值为1225；

当10≤t≤20时，y的取值范围是[600,1200]，当t＝20时，y取得最小值为600.

综上，第5天，日销售额y取得最大值为1225元；第20天，日销售额y取得最小值为600元．

10．某工厂生产某种产品，已知该产品的月生产量x(t)与1 t产品的价格p(元/t)之间的关系为p＝24200－x²，且生产x t的成本为R(元)，其中R＝50000+200x.问该厂每月生产多少吨产品才能使利润达到最大？最大利润是多少？(利润＝收入－成本)

解：每月生产x t时的利润为

f(x)＝(24200－x²)x－(50000+200x)

＝－x³+24000x－50000(x≥0)，

由f′(x)＝－x²+24000＝0，

解得x₁＝200，x₂＝－200(舍去)．

因f(x)在[0，+∞)内只有一个极值点x＝200且为极大值，故它就是最大值点，且最大值为f(200)＝－×(200)³+24000×200－50000＝3150000(元)．

故该厂每月生产200吨产品才能使利润达到最大且最大利润为3150000元．

9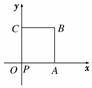．(2010·北京高考)如图放置的边长为1的正方形PABC沿x轴滚动．设顶点P(x，y)的纵坐标与横坐标的函数关系式是y＝f(x)，则f(x)的最小正周期为________；y＝f(x)在其两个相邻零点间的图象与x轴所围区域的面积为________．

说明：“正方形PABC沿x轴滚动”包括沿x轴正方向和沿x轴负方向滚动．沿x轴正方向滚动指的是先以顶点A为中心顺时计旋转，当顶点B落在x轴上时，再以顶点B为中心顺时针旋转，如此继续，类似地，正方形PABC可以沿x轴负方向滚动．

解析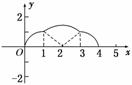：由题中信息可知无论正方形是沿着x轴的正方向还是负方向滚动，再次使点P与x轴接触的x轴方向的路程是4，故其最小正周期为4.在正方形的翻滚过程中，函数y＝f(x)的两个相邻零点间的图象如图所示．故其与x轴所围成的图形面积为S＝π×1²+×π×()²+2××1×1＝π+1.

答案：4　π+1