4．(文)已知函数f(x)＝g(x)＝log₂x，则f(x)与g(x)两函数图象的交点个数为(　)

A．4　 　　　　　　　　　　　　 B．3

C．2　 　　　　　　　　　　　　 D．1

解析：如图，函数g(x)的图象与函数f(x)的图象交于两点，且均在函数y＝8x－8(x≤1)的图象上．

答案：C

(理)已知函数f(x)＝，若方程f(x)＝k无实数根，则实数k的取值范围是(　)

A．(－∞，0)　 　　　　　　　　　　　　 B．(－∞，1)

C．(－∞，lg)　 　　　　　　　　　　　　　　 D．(lg，+∞)

解析：在同一坐标系内作出函数y＝f(x)与y＝k的图象，如图所示，若两函数图象无交点，则k<lg.

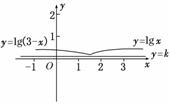
答案：C

3．(2011·重庆模拟)f(x)＝2^x－1的反函数是(　)

A．f^－1(x)＝log₂(x－1)　(x＞1)

B．f^－1(x)＝log₂(x+1)　(x＞－1)

C．f^－1(x)＝log₂(1－x)　(x＜1)

D．f^－1(x)＝1+log₂x　(x＞0)

解析：由y＝2^x－1得x＝log₂(1+y)，

又y＝f(x)＝2^x－1＞－1，

所以f^－1(x)＝log₂(x+1)　(x＞－1)．

答案：B

2．(2010·全国卷Ⅰ)设a＝log₃2，b＝ln2，c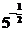＝，则(　)

A．a＜b＜c　 　　　　　　　　　　 B．b＜c＜a

C．c＜a＜b　 　　　　　　　　　　 D．c＜b＜a

解析：a＝log₃2＝＜ln 2＝b，又c＝5－＝＜，a＝log₃2＞log₃＝，因此c＜a＜b.

答案：C

1．(2010·辽宁高考)设2^a＝5^b＝m，且+＝2，则m＝(　)

A.　 　　　　　　　　　　　 B．10

C．20　 　　　　　　　　　　　 D．100

解析：a＝log₂m，b＝log₅m，代入已知得log_m2+log_m5＝2，即log_m10＝2，所以m＝.

答案：A

12．当x∈(1,2)时，不等式(x－1)²<log_ax恒成立，求a的取值范围．

解：设f₁(x)＝(x－1)²，f₂(x)＝log_ax，

要使当x∈(1,2)时，不等式(x－1)²<log_ax恒成立，

只需f₁(x)＝(x－1)²在(1,2)上的图象在f₂(x)＝log_ax的下方即可．

当0<a<1时，由图象知显然不成立．

当a>1时，如图，要使在(1,2)上，f₁(x)＝(x－1)²的图象在f₂(x)＝log_ax的下方，

只需f₁(2)≤f₂(2)，

即(2－1)²≤log_a2，log_a2≥1，∴1<a≤2.

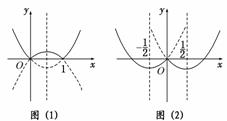
11．若直线y＝2a与函数y＝|a^x－1|(a>0且a≠1)的图象有两个公共点，求a的取值范围．

解：当0<a<1时，y＝|a^x－1|的图象如图(1)所示，由已知得0<2a<1，∴0<a<.

当a>1时，y＝|a^x－1|的图象如图(2)所示，

由已知可得0<2a<1，

∴0<a<，但a>1，故a∈∅.

综上可知，0<a<.

10．(1)作函数y＝|x－x²|的图象；

(2)作函数y＝x²－|x|的图象；

(3)作函数y＝()^|x|的图象．

解：(1)y＝

即y＝其图象如图(1)所示．

(2)y＝其图象如图(2)所示．

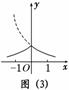
(3)作出y＝()^x的图象，保留y＝()^x图象中x≥0的部分，加上y＝()^x的图象中x>0的部分关于y轴的对称部分，即得y＝()^|x|的图象，如图(3)所示．

9．方程x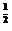＝()^x的实根个数是________．

解析：设f(x)＝x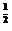，g(x)＝()^x，其图象如右，

由图象知，x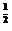＝()^x实根个数是1个．

答案：1

8．使log₂(－x)<x+1成立的x的取值范围是________．

解析：作出函数y＝log₂(－x)及y＝x+1的图象，

其中y＝log₂(－x)与y＝log₂x的图象关于y轴对称，观察图象知(如图所示)，－1<x<0，即x∈(－1,0)．

也可把原不等式化为后作图．

答案：(－1,0)

7．函数f(x)与g(x)的定义域为[m，n]，它们的图象如图所示，则不等式f(x)g(x)<0的解集是________．

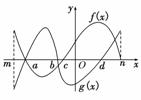
解析：f(x)·g(x)<0，等价于或

答案：[m，a)∪(a，b)∪(c，d)