2．(2011·北京模拟)函数f(x)＝x²－bx+c满足f(1+x)＝f(1－x)且f(0)＝3，则f(b^x)与f(c^x)的大小关系是(　)

A．f(b^x)≤f(c^x)

B．f(b^x)≥f(c^x)

C．f(b^x)>f(c^x)

D．大小关系随x的不同而不同

解析：∵f(1+x)＝f(1－x)，

∴f(x)的对称轴为直线x＝1，

由此得b＝2.

又f(0)＝3，∴c＝3.

∴f(x)在(－∞，1)上递减，在(1，+∞)上递增．

若x≥0，则3^x≥2^x≥1，

∴f(3^x)≥f(2^x)．

若x<0，则3^x<2^x<1，

∴f(3^x)>f(2^x)．

∴f(3^x)≥f(2^x)．

答案：A

1．函数y＝的图象大致是(　)

解析：法一：y＝＝.

法二：函数y＝的定义域为{x|x>0}．

答案：C

12．已知函数f(x)＝log_a(x+1)(a>1)，若函数y＝g(x)图象上任意一点P关于原点对称点Q的轨迹恰好是函数f(x)的图象．

(1)写出函数g(x)的解析式；

(2)当x∈[0,1)时总有f(x)+g(x)≥m成立，求m的取值范围．

解：(1)设P(x，y)为g(x)图象上任意一点，

则Q(－x，－y)是点P关于原点的对称点，

∵Q(－x，－y)在f(x)的图象上，

∴－y＝log_a(－x+1)，

即y＝g(x)＝－log_a(1－x)．

(2)f(x)+g(x)≥m，即log_a≥m，

设F(x)＝log_a，x∈[0,1)，

由题意，知只要F(x)_min≥m即可．

∵F(x)在[0,1)上是增函数，

∴F(x)_min＝F(0)＝0.

故m≤0即为所求．

w。w-w*k&s%5￥u

11．设a>0，a≠1，函数y＝有最大值，求函数f(x)＝log_a(3－2x－x²)的单调区间．

解：设t＝lg(x²－2x+3)＝lg[(x－1)²+2]．当x∈R时，t有最小值lg2.

又因为函数y＝有最大值，所以0<a<1.

因为f(x)＝log_a(3－2x－x²)的定义域为{x|－3<x<1}，令u＝3－2x－x²，x∈(－3,1)，则y＝log_au.

因为y＝log_au在定义域内是减函数，当x∈(－3，－1]时，u＝－(x+1)²+4是增函数，所以f(x)在(－3，－1]上是减函数．同理，f(x)在[－1,1)上是增函数．

故f(x)的单调减区间为(－3，－1]，单调增区间为[－1,1)．

10．(1)已知log_a2＝m，log_a3＝n，求a^2m+n的值；

(2)已知2lg＝lg x+lg y，求 的值．

解：(1)由log_a2＝m，log_a3＝n得a^m＝2，aⁿ＝3，

∴a^2m+n＝a^2m·aⁿ＝2²×3＝12.

(2)由已知得lg()²＝lg(xy)，

∴()²＝xy，即x²－6xy+y²＝0，

∴()²－6·+1＝0，

∴＝3±2.

∵

∴>1，从而＝3+2，

∴＝1+.

9．已知函数f(x)满足：当x≥4时，f(x)＝()^x；当x<4时，f(x)＝f(x+1)，则f(2+log₂3)＝________.

解析：∵3<2+log₂3<4，

∴f(2+log₂3)＝f(3+log₂3)＝()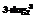

＝×()＝×()＝×＝.

答案：

8．设m为常数，如果函数y＝lg(mx²－4x+m－3)的值域为R，则m的取值范围是________．

解析：因为函数值域为R，所以mx²－4x+m－3能取到所有大于0的数，即满足或m＝0.解得0≤m≤4.

答案：[0,4]

7．－×log₂+2lg(+)的结果为________．

解析：原式＝9－3×(－3)+lg(+)²＝18+lg10＝19.

答案：19

6．设函数f(x)＝lg(x²+bx－b－1)，给出下述命题：

①f(x)有最小值；②当b＝0时，f(x)的值域为R；③若f(x)在区间[2，+∞)内单调递增，则实数b的取值范围是b≥－4；④函数f(x)的定义域和值域可以同时为R.其中正确命题的个数是(　)

A．1　 　　　　　　　　　　　　 B．2

C．3　 　　　　　　　　　　　　 D．4

解析：当x²+bx－b－1接近零时，f(x)无最小值，所以①不正确；当b＝0时，x²－1取遍所有的正数，从而f(x)的值域为R，所以②正确；若f(x)在[2，+∞)内单调递增，则应有4+2b－b－1>0，得b>－3，所以③不正确；值域为R时，应有Δ≥0，定义域为R时，应有Δ<0，所以④不正确．

答案：A

5．(2011·深圳模拟)若函数f(x)＝log_a(x+b)的大致图象如图所示，其中a，b(a>0且a≠1)为常数，则函数g(x)＝a^x+b的大致图象是(　)

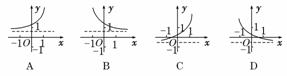
解析：由图可知，函数f(x)＝log_a(x+b)是单调递减函数，所以0<a<1，又因为f(x)＝log_a(x+b)的图象与x轴的交点的横坐标在(0,1)内，所以0<b<1，根据上述参数a，b的特点，函数g(x)＝a^x+b的图象大致如B项所示．

答案：B