15．已知正数a、b满足a+b＝1.

(1)求ab的取值范围；

(2)求ab+的最小值．

分析：若等号不能成立，则考查相关函数的单调性．

解析：(1)由≥，得0＜ab≤.

(2)设函数f(x)＝x+(0＜x≤)，x＝ab

设0＜x₁＜x₂≤，

f(x₁)－f(x₂)＝(x₁+)－(x₂+)

＝(x₁－x₂)+(－)

＝(x₁－x₂)(1－)

∵0＜x₁＜x₂≤，x₁－x₂＜0，

x₁x₂＜，1－＜0，

∴(x₁－x₂)(1－)＞0.

∴f(x₁)＞f(x₂)．

即f(x)在(0，]上是减函数，

因此当x＝时，f(x)取得最小值4+＝.

总结评述：函数f(x)＝x+(a＞0)是一个重要的函数，应了解它的变化．f(x)＝x+(a＞0)在(0，]上是减函数，在[，+∞)上是增函数．在研究此函数的过程中，应先确定它的定义域，若x＝成立，则可由极值定理求极值；若x＝不成立，则应在定义域内研究f(x)的单调性．

14．某小区欲建一面积为640平方米的矩形绿地，四周有小路，绿地长边外小路宽5米，短边外小路宽8米(如下图所示)．求怎样设计绿地的长宽使绿地和小路总占地面积最小？

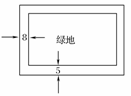
解析：设绿地的长边为x米，则宽边为米，总占地为S平方米．

S＝(x+16)(+10)

＝10x++800

≥2+800＝1440

当且仅当10x＝，即x＝32米，＝20米时，上式中等号成立．

因此，当绿地的长宽分别为32米，20米时，绿地和小路总占地面积最小为1440平方米．

13．解下列问题：

(1)已知a＞0，b＞0，且4a+b＝1，求ab的最大值；

(2)已知x＞2 ，求x+的最小值；

(3)已知x＞0，y＞0，且x+y＝1，求+的最小值．

解析：(1)法一：∵a＞0，b＞0,4a+b＝1，

∴1＝4a+b≥2＝4，

当且仅当4a＝b＝，即a＝，b＝时，等号成立．

∴≤，

∴ab≤.

所以ab的最大值为.

法二：∵a＞0，b＞0,4a+b＝1，

∴ab＝·4a·b≤()²＝，

当且仅当4a＝b＝，即a＝，b＝时，等号成立．

所以ab的最大值为.

(2)∵x＞2，

∴x－2＞0，

∴x+＝x－2++2

≥2+2＝6，

当且仅当x－2＝，即x＝4时，等号成立．

所以x+的最小值为6.

(3)∵x＞0，y＞0，x+y＝1，

∴+＝(x+y)(+)＝13++

≥13+2＝25，

当且仅当＝时等号成立，由

得

∴当x＝，y＝时取等号．所以+的最小值为25.

12．(2009·江苏南通二模，6)在下面等号右侧两个分数的分母括号处，各填上一个自然数，使等式成立且这两个自然数的和最小：1＝+，所填自然数分别为________．

答案：4,12

解析：设这两个自然数为a，b，则1＝+，a+b＝(a+b)(+)＝10++≥16，当且仅当b＝3a时取等号，此时求得a＝4，b＝12，故填4,12.

11．(2009·浙江宁波名校一模)已知圆C：x²+y²+bx+ay－3＝0(a，b为正实数)上任意一点关于直线l：x+y+2＝0的对称点都在圆C上，则+的最小值为________．

答案：1+

解析：由题意知直线l过圆心(－，－)，

∴－－+2＝0，

即a+b＝4，∴+＝1，

∴+＝(+)(+)＝+++＝1+(+)≥1+.

10．已知a，b，c∈R⁺，则(a+b+c)(+)的最小值是________．

答案：4

解析：∵(a+b+c)(+)＝[(a+b)+c](+)＝1+++1＝2+(+)，

又∵a，b，c∈R⁺，∴+≥2.

∴(a+b+c)(+)≥4.∴最小值为4.

9．(2009·吉林长春一模)若正数a、b满足+＝2，则ab的最小值为________．

答案：4

解析：∵a、b都为正数．

∴2＝+≥2＝，∴ab≥4.

8．已知m，n，s，t∈R⁺，m+n＝2，+＝9，其中m，n是常数，且s+t的最小值是，满足条件的点(m，n)是椭圆+＝1一弦的中点，则此弦所在的直线方程为　　　　　　 (　)

A．x－2y+1＝0　 　　　　　　　　　　 B．2x－y－1＝0

C．2x+y－3＝0　 　　　　　　　　　　 D．x+2y－3＝0

答案：D

解析：由已知得s+t＝(s+t)(+)＝(m+n++)≥(m+n+2)＝(+)²，又s+t的最小值是，因此(+)²＝，+＝2，又m+n＝2，所以m＝n＝1.设以点(m，n)为中点的弦的两个端点的坐标分别是(x₁，y₁)、(x₂，y₂)，则有+＝1，

+＝1，

两式相减得+＝0　①，又点(1,1)是该弦的中点，因此有＝＝1，x₁+x₂＝y₁+y₂＝2　②，把②代入①得＝－，即所求直线的斜率是－，所求直线的方程是y－1＝－(x－1)，即x+2y－3＝0.

总结评述：在求解有关二次曲线的以某个已知点为中点的弦所在的直线方程时，注意利用“点差法”来确定相应直线的斜率．

7．设0＜x＜1，a，b都为大于零的常数，则+的最小值为　　　　　　　　　　 (　)

A．(a－b)²　 　　　　　　　　　　　　　　 B．(a+b)²

C．a²b²　 　　　　　　　　　　　　　　　　　 D．a²

答案：B

解析：+＝(+)[x+(1－x)]＝a²+b²++≥a²+b²+2＝(a+b)²，故选B.

6．(2009·天津，9)设x，y∈R，a＞1，b＞1.若a^x＝b^y＝3，a+b＝2，则+的最大值为　　　　　　　　　　　　　　　　　　　 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　)

A．2　 　　　　　　　　 B.　 　　　　　　　　　　　　　 C．1　 　　　　　　　　　　　　 D.

答案：C

解析：∵a^x＝b^y＝3，∴x＝log_a3，y＝log_b3，

∴+＝+＝log₃a+log₃b＝log₃ab≤log₃＝log₃3＝1，故选C.