4．(2009·安徽皖北联考)已知三棱锥的三个侧面两两垂直，三条侧棱长分别为4,4,7，若此三棱锥的各个顶点都在同一球面上，则此球的表面积是　　　　　　　　　　　　　　　　　　　 (　)

A．81π　 B．36π　 C.π　 D．144π

答案：A

解析：由于三棱锥的三个侧面两两垂直，即可把它补成长方体，其对角线长为9，外接球的半径为，则球的表面积为81π，故选A.

3．(2009·东北三省十校一模)三棱锥P－ABC中∠ABC＝90°，PA＝PB＝PC，则下列说法正确的是　　　　　　　　　　　　　 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　)

A．平面PAC⊥平面ABC　 　　　　　　　　　　　 B．平面PAB⊥平面PBC

C．PB⊥平面ABC　 　　　　　　　　　　　　　　　 D．BC⊥平面PAB

答案：A

解析：如图，因为∠ABC＝90°，PA＝PB＝PC，所以点P在底面的射影落在△ABC的斜边的中点O处，连结OB、OP，则PO⊥OB.又∵PA＝PC，所以PO⊥AC，且AC∩OB＝O，

所以PO⊥平面ABC.

又∵PO⊂平面PAC，∴平面PAC⊥平面ABC，故选A.

2．(2009·广东重点中学)已知三条不重合的直线m、n、l与两个不重合的平面α、β，有下列命题：

①若m∥n，n⊂α，则m∥α；

②若l⊥α，m⊥β且l∥m，则α∥β；

③若m⊂α，n⊂α，m∥β，n∥β，则α∥β；

④若α⊥β，α∩β＝m，n⊂β，n⊥m，则n⊥α.

其中正确的命题个数是　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　)

A．1　　　B．2　　　C．3　　　D．4

答案：B

解析：对于①，若m∥n，n⊂α，则m∥α或m⊂α，①不正确；对于②，若l⊥α，m⊥β且l∥m，则α∥β，显然成立；对于③，若m⊂α，n⊂α，m∥β，n∥β，则α∥β，由面面平行的判定定理知它是不正确的；对于④，若α⊥β，α∩β＝m，n⊂β，n⊥m，则n⊥α，由面面垂直的性质定理知它是正确的；综上所述，正确命题的个数为2，故选B.

1．(2009·上海市普通高等学校春季招生考试)在空间中，“两条直线没有公共点”是“这两条直线平行”的　　　　　　 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　)

A．充分不必要条件　　　　　　　　 B．必要不充分条件

C．充要条件　 　　　　　　　　　　　　　　　　 D．既不充分也不必要条件

答案：B

解析：在空间中，两条直线没有公共点，这两条直线可能是异面直线，即由“两条直线没有公共点”不能推知“这两条直线平行”；反过来，由“两条直线平行”可知“这两条直线没有公共点”．因此，在空间中，“两条直线没有公共点”是“这两条直线平行”的必要不充分条件，选B.

16．如图所示，在正方体ABCD－A₁B₁C₁D₁中，O，M分别是BD₁，AA₁的中点．

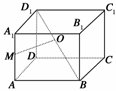
(1)求证：MO是异面直线AA₁和BD₁的公垂线；

(2)求异面直线AA₁与BD₁所成的角的余弦值；

(3)若正方体的棱长为a，求异面直线AA₁与BD₁的距离．

解析：(1)证明：∵O是BD₁的中点，

∴O是正方体的中心，

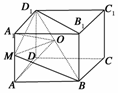∴OA＝OA₁，

又M为AA₁的中点，

即OM是线段AA₁的垂直平分线，

故OM⊥AA₁.

连结MD₁、BM，则可得MB＝MD₁.

同理由点O为BD₁的中点知MO⊥BD₁，

即MO是异面直线AA₁和BD₁的公垂线．

(2)由于AA₁∥BB₁，

所以∠B₁BD₁就是异面直线AA₁和BD₁所成的角．

在Rt△BB₁D₁中，设BB₁＝1，则BD₁＝，

所以cos∠B₁BD₁＝，

故异面直线AA₁与BD₁所成的角的余弦值等于.

(3)由(1)知，所求距离即为线段MO的长，

由于OA＝AC₁＝a，AM＝，且OM⊥AM，所以OM＝a.

15．如图，在直三棱柱ABC－A₁B₁C₁中，AB＝BC＝B₁B＝a，∠ABC＝90°，D、E分别为BB₁、AC₁的中点．

(1)求异面直线BB₁与AC₁所成的角的正切值；

(2)证明：DE为异面直线BB₁与AC₁的公垂线；

(3)求异面直线BB₁与AC₁的距离．

解析：(1)由于直三棱柱ABC－A₁B₁C₁中，AA₁∥BB₁，所以∠A₁AC₁就是异面直线BB₁与AC₁所成的角．

又AB＝BC＝B₁B＝a，∠ABC＝90°，

所以A₁C₁＝a，tan∠A₁AC₁＝，

即异面直线BB₁与AC₁所成的角的正切值为.

(2)证明：解法一：如图，在矩形ACC₁A₁中，过点E作AA₁的平行线MM₁分别交AC、A₁C₁于点M、M₁，连结BM，B₁M₁，则BB₁綊MM₁.

又D、E分别是BB₁、MM₁的中点，

可得DE綊BM.

在直三棱柱ABC－A₁B₁C₁中，

由条件AB＝BC得BM⊥AC，

所以BM⊥平面ACC₁A₁，

故DE⊥平面ACC₁A₁，所以DE⊥AC₁，DE⊥BB₁，

即DE为异面直线BB₁与AC₁的公垂线．

解法二：如图，延长C₁D、CB交于点F，连结AF，由条件易证D是C₁F的中点，B是CF的中点，又E是AC₁的中点，所以DE∥AF.

在△ACF中，由AB＝BC＝BF知AF⊥AC.

在直三棱柱ABC－A₁B₁C₁中，AA₁⊥平面ABC，

所以AF⊥AA₁，故AF⊥平面ACC₁A₁，

故DE⊥平面ACC₁A₁，所以DE⊥AC₁，DE⊥BB₁，

即DE为异面直线BB₁与AC₁的公垂线．

(3)由(2)知线段DE的长就是异面直线BB₁与AC₁的距离，由于AB＝BC＝a，∠ABC＝90°，

所以DE＝a.

反思归纳：两条异面直线的公垂线是指与两条异面直线既垂直又相交的直线，两条异面直线的公垂线是惟一的，两条异面直线的公垂线夹在两条异面直线之间的线段的长度就是两条异面直线的距离．证明一直线是某两条异面直线的公垂线，可以分别证明这条直线与两条异面直线垂直．本题的思路是证明这条直线与一个平面垂直，而这一平面与两条异面直线的位置关系是一条直线在平面内，另一条直线与这个平面平行．

14．如下图所示，在棱长为1的正方体ABCD－A₁B₁C₁D₁中，M为AB的中点，N为BB₁的中点，O为面BCC₁B₁的中心．

(1)过O作一直线与AN交于P，与CM交于Q(只写作法，不必证明)；

(2)求PQ的长(不必证明)．

解析：(1)由ON∥AD知，AD与ON确定一个平面α.又O、C、M三点确定一个平面β(如下图所示)．

∵三个平面α，β和ABCD两两相交，有三条交线OP、CM、DA，其中交线DA与交线CM不平行且共面．

∴DA与CM必相交，记交点为Q.

∴OQ是α与β的交线．连结OQ与AN交于P，与CM交于Q，

故OPQ即为所作的直线．

(2)解三角形APQ可得PQ＝.

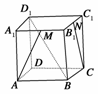
13．如图所示，正方体ABCD－A₁B₁C₁D₁中，M、N分别是A₁B₁，B₁C₁的中点．问：

(1)AM和CN是否是异面直线？说明理由；

(2)D₁B和CC₁是否是异面直线？说明理由．

解析：(1)由于M、N分别是A₁B₁和B₁C₁的中点，可证明MN∥AC，因此AM与CN不是异面直线．(2)由空间图形可感知D₁B和CC₁为异面直线的可能性较大，判断的方法可用反证法．

探究拓展：解决这类开放型问题常用的方法有直接法(即由条件入手，经过推理、演算、变形等)，如第(1)问，还有假设法，特例法，有时证明两直线异面用直线法较难说明问题，这时可用反证法，即假设两直线共面，由这个假设出发，来推证错误，从而否定假设，则两直线是异面的．

解：(1)不是异面直线．理由如下：

∵M、N分别是A₁B₁、B₁C₁的中点，∴MN∥A₁C₁.

又∵A₁A∥D₁D，而D₁D綊C₁C，

∴A₁A綊C₁C，∴四边形A₁ACC₁为平行四边形．

∴A₁A∥AC，得到MN∥AC，

∴A、M、N、C在同一个平面内，故AM和CN不是异面直线．

(2)是异面直线．理由如下：

假设D₁B与CC₁在同一个平面CC₁D₁内，

则B∈平面CC₁D₁，C∈平面CC₁D₁.

∴BC⊂平面CC₁D₁，这与在正方体中BC⊥平面CC₁D₁相矛盾，

∴假设不成立，故D₁B与CC₁是异面直线．

12．(2009·北京海淀一模)已知四面体P－ABC中，PA＝PB＝PC，且AB＝AC，∠BAC＝90°，则异面直线PA与BC所成的角为________．

答案：90°

解析：如图，因为△ABC是直角三角形，所以点P在底面的射影一定落在Rt△ABC斜边的中点上，设为点M，连结PM、AM.又因为AB＝AC，所以AM与BC垂直，由三垂线定理可知PA与BC垂直，所以PA与BC所成的角为90°.

11．设a，b，c是空间的三条直线，下面给出四个命题：

①若a⊥b，b⊥c，则a∥c；

②若a、b是异面直线，b、c是异面直线，则a、c也是异面直线；

③若a和b相交，b和c相交，则a和c也相交．

④若a和b共面，b和c共面，则a和c也共面．

其中真命题的个数是________个．

答案：0

解析：∵a⊥b，b⊥c

∴a与c可以相交、平行、异面，故①错；

又∵a，b异面，b，c异面，则a，c异面、相交、平行，故②错；

由a、b相交，b、c相交，则a、c可以异面，故③错；

同理④错，故真命题个数为0个．