4．(2009·东北三省十校一模)三棱锥P－ABC中∠ABC＝90°，PA＝PB＝PC，则下列说法正确的是　　　　　　　　　　　　　 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　)

A．平面PAC⊥平面ABC　　　 B．平面PAB⊥平面PBC

C．PB⊥平面ABC　　　　　　 D．BC⊥平面PAB

答案：A

解析：如图，因为∠ABC＝90°，PA＝PB＝PC，所以点P在底面的射影落在△ABC的斜边的中点O处，连结OB、OP，则PO⊥OB.又∵PA＝PC，所以PO⊥AC，且AC∩OB＝O，所以PO⊥平面ABC.

又∵PO⊂平面PAC，∴平面PAC⊥平面ABC，故选A.

3．(2009·北京海淀一模)已知l是直线，α、β是两个不同的平面，下列命题中真命题的是

(　)

A．若l∥α，l∥β，则α∥β　　　 B．若α⊥β，l∥α，则l⊥β

C．若l⊥α，l∥β，则α⊥β　　　 D．若l∥α，α∥β，则l∥β

答案：C

解析：选项A中，如图①，α与β可能相交，所以A不正确；选项B中，如图②，l与β可能平行，所以B不正确；选项D中，如图③，可能有l⊂β，所以D不正确，故选C.

2．(2009·北京宣武一模)若a，b是空间两条不同的直线，α，β是空间的两个不同的平面，则a⊥α的一个充分不必要条件是　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　)

A．a∥β，α⊥β　　　　　　 B．a⊂β，α⊥β

C．a⊥b，b∥α　 　　　　　　　　　　　 D．a⊥β，α∥β

答案：D

解析：选项A中，若a∥β，α⊥β，直线a与平面α可能平行，如图①，所以A不正确；选项B中，若a⊂β，α⊥β，直线a与α可能平行，可能相交，可能为包含关系，如图②，所以B不正确；选项C中，a⊥b，b∥α，直线a与α可能平行，如图③，所以C不正确，故选D.

1．(2009·山东，5)已知α，β表示两个不同的平面，m为平面α内的一条直线，则“α⊥β”是“m⊥β”的　　　　　　　　 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 　　　 (　)

A．充分不必要条件　　　　　 B．必要不充分条件

C．充要条件　　　　　　　　 D．既不充分也不必要条件

答案：B

解析：由面面垂直的判定定理可知必要性成立，而当两平面α、β垂直时，α内的直线m只有在垂直于两平面的交线时才垂直于另一个平面β，∴充分性不成立，故选B.

16．如图所示，直三棱柱ABC－A′B′C′中，AC＝BC＝AA′，∠ACB＝90°，D、E分别为AB、BB′的中点．

(1)求证：CE⊥A′D；

(2)求异面直线CE与AC′所成角的余弦值．

解析：(1)设＝a，＝b，＝c，

根据题意，|a|＝|b|＝|c|且a·b＝b·c＝c·a＝0，

∴＝b+c，＝－c+b－a.

∴·＝－c²+b²＝0.

∴CE⊥A′D.

(2)＝－a+c，

∴||＝|a|，||＝|a|.

·＝(－a+c)·(b+c)＝c²＝|a|²，

∴cos?，?＝＝.

∴异面直线CE与AC′所成角的余弦值为.

15．正方体ABCD－A₁B₁C₁D₁中，E、F分别是BB₁、D₁B₁的中点，求证：EF⊥平面AB₁C.

证明：证法一：设＝a，＝c，＝b，

则＝+＝(+)

＝(+)＝(+－)

＝(－a+b+c)．

∵＝+＝a+b，

∴·＝(－a+b+c)·(a+b)

＝(－a²+a·b+a·c+a·b+b²+b·c)

∵a²＝|a|²，b²＝|b|²，

∴b²－a²＝0.又a·c＝b·c＝0，

∴·＝0，

∴⊥.同理可证⊥.

∴EF⊥AB₁，EF⊥B₁C，从而EF⊥平面B₁AC.

证法二：设正方体的棱长为2，如图以D为原点建立空间直角坐标系，

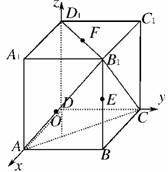
则A(2,0,0)，C(0,2,0)，B₁(2,2,2)，E(2,2,1)，F(1,1,2)，

∴＝(1,1,2)－(2,2,1)＝(－1，－1,1)，

＝(0,2,2)，＝(－2,2,0)．

·＝－1×0+(－1)×2+1×2＝0，

∴⊥，同理⊥，

即EF⊥AB₁，EF⊥AC

∴EF⊥平面B₁AC.

总结评述：证法一利用了向量之间的转化，重在逻辑推理，上面的证法二利用了向量的坐标运算，重点在于计算．这两种方法是立体几何中证明平行或垂直最常用的方法，都应予以掌握．

14．已知空间四边形ABCD的每条边和对角线长都等于a，点E、F、G分别是AB、AD、DC的中点，求下列向量的数量积．

(1)·；

(2)·；

(3)·；

(4)·.

解析：在空间四边形ABCD中，

||＝||＝a，〈，〉＝60°；

(1)∴·＝a·acos60°＝a².

(2)||＝a，||＝a，〈，〉＝60°.

∴·＝a²cos60°＝a².

(3)||＝a，||＝a，又∥，

∴〈，〉＝π，

∴·＝a²cosπ＝－a².

(4)∵||＝a，||＝a，EF∥BD，

∴〈，〉＝〈，〉＝60°.

∴·＝a²cos60°＝a².

13．如图所示，设P是正方形ABCD所在平面外一点，O为正方形ABCD的中心，Q是CD的中点，已知PO⊥平面ABCD.

(1)用基向量P、P、P表示向量O；

(2)用基向量P、P、P表示向量P.

解析：(1) O＝P－P＝P－(P+P)＝－P－P+P.

(2)∵P+P＝2P，∴P＝2P－P.

又∵P+P＝2P，∴P＝2P－P.

∴P＝2P－P＝2P－(2P－P)

＝2P－2P+P.

12．在各棱长都等于1的正四面体OABC中，若点P满足＝x·+y·+z·(x+y+z＝1)，则||的最小值等于______．

答案：

解析：由于点P满足＝x·OA+y·+z·(x+y+z＝1)，所以点P与A，B，C共面，即P点在平面ABC内，所以||的最小值即为点O到平面ABC的距离，亦即正四面体的高，可以求得||的最小值为.

11．已知平行六面体ABCD-A′B′C′D′中，以顶点A为端点的三条棱长都等于1，且两两夹角都是60°，则对角线AC₁的长是________．

答案：

解析：||²＝²＝(++)²＝²+²+²+2·+2·+2·＝1+1+1+2·+2·+2·＝6.则|AG|＝.