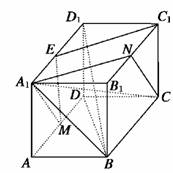
14．如图，长方体ABCD－A₁B₁C₁D₁中，AB＝AA₁＝a，BC＝a，M是AD中点，N是B₁C₁中点．

(1)求证：A₁、M、C、N四点共面；

(2)求证：BD₁⊥MC；

(3)求证：平面A₁MCN⊥平面A₁BD₁；

(4)求A₁B与平面A₁MCN所成的角．

解析：(1)取A₁D₁中点E，连结ME、C₁E，∴A₁N綊EC₁，MC綊EC₁.

∴A₁N綊MC.

∴A₁，M，C，N四点共面．

(2)连结BD，则BD是BD₁在平面ABCD内的射影．

∵＝＝＝，

∴Rt△CDM∽Rt△BCD，

∠DCM＝∠CBD.

∴∠CBD+∠BCM＝90°.

∴MC⊥BD.∴BD₁⊥MC.

(3) 连结A₁C，由A₁BCD₁是正方形，知BD₁⊥A₁C.

∵BD₁⊥MC，∴BD₁⊥平面A₁MCN.

∴平面A₁MCN⊥平面A₁BD₁.

(4)∠BA₁C是A₁B与平面A₁MCN所成的角且等于45°.

13．如图，在四棱锥P－ABCD中，PA⊥底面ABCD，AB⊥AD，AC⊥CD，∠ABC＝60°，PA＝AB＝BC，E是PC的中点．证明：

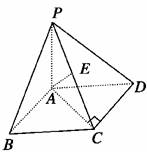
(1)CD⊥AE；

(2)PD⊥平面ABE.

证明：(1)在四棱锥P－ABCD中，

∵PA⊥底面ABCD，CD⊂平面ABCD，∴PA⊥CD.

∵AC⊥CD，PA∩AC＝A，∴CD⊥平面PAC.

而AE⊂平面PAC，∴CD⊥AE.

(2)由PA＝AB＝BC，∠ABC＝60°，可得AC＝PA.

∵E是PC的中点，∴AE⊥PC.

由(1)知，AE⊥CD，且PC∩CD＝C，∵AE⊥平面PCD.

而PD⊂平面PCD，∴AE⊥PD.

∵PA⊥底面ABCD，∴PA⊥AB.

又∵AB⊥AD，且PA∩AD＝A，

∴AB⊥平面PAD，而PD⊂平面PAD，∴AB⊥PD.

又∵AB∩AE＝A，综上可得PD⊥平面ABE.

12．(2009·江苏，12)设α和β为不重合的两个平面，给出下列命题：

(1)若α内的两条相交直线分别平行于β内的两条直线，则α平行于β；

(2)若α外一条直线l与α内的一条直线平行，则l和α平行；

(3)设α和β相交于直线l，若α内有一条直线垂直于l，则α和β垂直；

(4)直线l与α垂直的充分必要条件是l与α内的两条直线垂直．

上面命题中，真命题的序号是________(写出所有真命题的序号)．

答案：(1)(2)

解析：由面面平行的判定定理可知，(1)正确．

由线面平行的判定定理可知，(2)正确．

对于(3)来说，α内直线只垂直于α和β的交线l，得不到其是β的垂线，故也得不出α⊥β.

对于(4)来说，l只有和α内的两条相交直线垂直，才能得到l⊥α.

也就是说当l垂直于α内的两条平行直线的话，l不一定垂直于α.

11．对于四面体ABCD，给出下列四个命题：

①若AB＝AC，BD＝CD，则BC⊥AD；

②若AB＝CD，AC＝BD，则BC⊥AD；

③若AB⊥AC，BD⊥CD，则BC⊥AD；

④若AB⊥CD，AC⊥BD，则BC⊥AD.

其中真命题的序号是________．(把你认为正确命题的序号都填上)

答案：①④

解析：本题考查四面体的性质，取BC的中点E，则BC⊥AE，BC⊥DE，∴BC⊥面ADE，∴BC⊥AD，故①正确．设O为A在面BCD上的射影，依题意OB⊥CD，OC⊥BD，∴O为垂心，∴OD⊥BC，∴BC⊥AD，故④正确，②③易排除，故答案为①④.

10．在三棱锥P－ABC中，∠ABC＝90°，∠BAC＝30°，BC＝5，又PA＝PB＝PC＝AC，则点P到平面ABC的距离是________．

答案：5

解析：∵∠ABC＝90°，∠BAC＝30°，BC＝5，

∴AC＝10.

又PA＝PB＝PC＝AC＝10，

∴P在平面ABC内的射影是△ABC的外心，

即斜边AC中点，设为O，显然PO＝5.

9．如右图所示，PA⊥矩形ABCD所在的平面，那么以P、A、B、C、D五个点中的三点为顶点的直角三角形的个数是________．

答案：9个

解析：C－1＝10－1＝9，(包括△PBD，为什么说△PBD不为Rt△)

易判断∠PDB≠90°.

∠PBD≠90°，只须判断∠BPD≠90°.

假设∠BPD＝90°，设PA＝a，AD＝b，AB＝c.

∴PB²＝a²+c²，PD²＝a²+b²

∵∠BPD＝90°，∴BD²＝b²+c²+2a²

而由Rt△ABD得：BD²＝b²+c².

这显然不成立．∴∠BPD≠90°.

综合而得：△PBD不是Rt△，共有9个．

8．(2009·四川，5)如图所示，已知六棱锥P－ABCDEF的底面是正六边形，PA⊥平面ABC，PA＝2AB，则下列结论正确的是　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　)

A．PB⊥AD　　　　　　 B．平面PAB⊥平面PBC

C．直线BC∥平面PAE　　 D．直线PD与平面ABC所成的角为45°

答案：D

解析：∵PB在底面的射影为AB，AB与AD不垂直，∴PB与AD不垂直，排除A.又BD⊥AB，BD⊥PA，∴BD⊥面PAB.但BD不在面PBC内，排除B.∵BD∥AE，∴BD∥面PAE，∴BC与面PAE不平行，排除C.又∵PD与面ABC所成的角为∠PDA，∵AD＝2AB＝PA，∴∠PDA＝45°，故答案选D.

7．(2010·湖北八校联考)在下列四个正方体中，能得出AB⊥CD的是　　　　　　　　 (　)

答案：A

解析：∵CD在平面BCD内，AB是平面BCD的斜线，由三垂线定理可得A.

6．已知二面角α-l-β的大小为30°，m、n为异面直线，m⊥平面α，n⊥平面β，则m、n所成的角为　　　　　　　　　 　　　　　　　　　　　　　　　　　　　　　　　　 　　　　　　　　　　　　　　　　　　　　　 (　)

A．30° 　　　　 　B．60°　　　　 C．120° 　　　　　　　 　D．150°

答案：A

解析：∵m⊥α，n⊥β，∴m，n所成的夹角与二面角α-l-β所成的角相等或互补．

∵二面角α-l-β为30°，故异面直线m，n所成的夹角为30°，故选A.

5．给出下列四个命题：

①直线垂直于一个平面内的无数条直线是这条直线与这个平面垂直的充要条件；

②过空间一定点有且只有一条直线与已知平面垂直；

③不在一个平面内的一条直线和平面内的一条直线平行是这条直线和这个平面平行的充分条件；

④一个二面角的两个半平面分别垂直于另一个二面角的两个半平面，则这两个二面角相等或互补．

其中真命题为　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 　　　　　　　　　　　　　　 (　)

A．①③ 　B．②④　　　 C．②③　 　D．③④

答案：C

解析：①是必要条件，④相等或互补或不确定，如图．

面ABCD⊥面BEFC，面ECDG⊥面BEFC.

此时二面角A－BC－F与二面角G－EC－B的大小关系不确定，故选C.