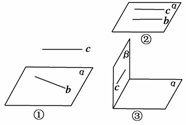
2．(2009·浙江宁波十校联考)设b，c表示两条直线，α，β表示两个平面，则下列命题是真命题的是　　　　　　　　　　　　 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　)

A．若b⊂α，c∥α，则b∥c　　　　　　　 B．若b⊂α，b∥c，则c∥α

C．若c∥α，α⊥β，则c⊥β　　　　　　　 D．若c∥α，c⊥β，则α⊥β

答案：D

解析：选项A中，如图①，b⊂α，c∥α，直线b与c异面，所以A不正确；选项B中，如图②，直线c可能在平面α内，所以B不正确；选项C中，如图③，直线c可能在平面β内，所以C不正确．故选D.

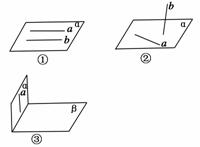
1．(2009·北京西城一模)已知直线a和平面α，那么a∥α的一个充分条件是　　 (　)

A．存在一条直线b，a∥b，b⊂α

B．存在一条直线b，a⊥b，b⊥α

C．存在一个平面β，a⊂β，α∥β

D．存在一个平面β，a⊥β，α⊥β

答案：C

解析：选项A中，若a∥b，b⊂α可能有a⊂α，如图①，所以A不正确；

选项B中，若a⊥b，b⊥α可能有a⊂α，如图②，所以B不正确；

选项D中，可能有a⊂α，如图③，所以D不正确．故选C.

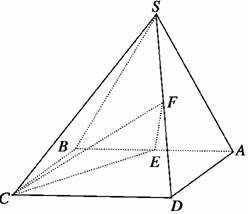
16．(2009·河北唐山一模)如图所示，四棱锥S－ABCD的底面ABCD是正方形，侧面SAB是等腰三角形且垂直于底面，SA＝SB＝，AB＝2，E、F分别是AB、SD的中点．

(1)求证：EF∥平面SBC；

(2)求二面角F－CE－A的大小．

解析：解法一：(1)证明：如图(1)，取SC中点G，连结FG、BG，则FG綊CD.

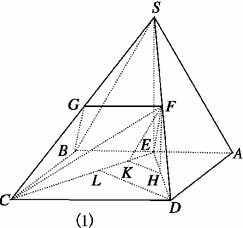
又BE綊CD，∴FG綊BE，四边形BEFG是平行四边形，∴EF∥BG.又∵EF⊄平面SBC，BG⊂平面SBC，∴EF∥平面SBC.

(2)连结SE，

∵SA＝SB，∴SE⊥AB.

又∵平面SAB⊥平面ABCD，∴SE⊥平面ABCD.而SE⊂平面SDE，

∴平面SDE⊥平面ABCD.

作FH⊥DE于H，则FH⊥平面ABCD，

且FH∥SE，H为DE的中点．

作HK⊥CE于K，连结FK，则CE⊥FK.

于是∠FKH为二面角F－CE－A的平面角．

∵SA＝SB＝，AB＝2，

∴SE＝2，FH＝1.

在正方形ABCD中，作DL⊥CE于L，则

DL＝CDsin∠LCD＝CDsin∠BEC＝2×＝2×＝.

∴HK＝DL＝，

∴tan∠FKH＝＝.

解法二：如图(2)，以E为原点，建立空间直角坐标系，使BC∥x轴，A、S分别在y轴、z轴上．

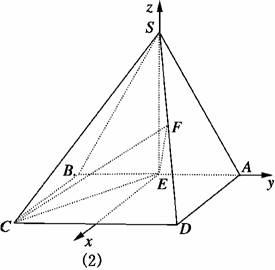
(1)证明：由已知，E(0,0,0)，D(2,1,0)，

S(0,0,2)，F(1，，1)，B(0，－1,0)，

C(2，－1,0)，∴E＝(1，，1)，

B＝(2,0,0)，B＝(0,1,2)．∵E＝B+B，EF⊄平面SBC，

∴EF∥平面SBC.

(2)设m＝(a，b，c)为平面CEF的法向量，

则m⊥E，且m⊥E.

∵E＝(2，－1,0)，E＝(1，，1)，

则m·E＝m·E＝0，

∴取a＝1，b＝2，c＝－2，

则m＝(1,2，－2)．

又∵n＝(0,0,1)为平面ACE的法向量，

所以cos〈m，n〉＝＝＝－，

因为二面角F－CE－A为锐角，所以其大小为arccos.

15．(2009·河北秦皇岛一模)如图所示，在直四棱柱ABCD－A₁B₁C₁D₁中，AA₁＝2，底面是边长为1的正方形，E、F、G分别是棱BB₁、DD₁、DA的中点．

(1)求证：平面AD₁E∥平面BGF；

(2)求证：D₁E⊥平面AEC.

证明：(1)∵E、F分别是棱BB₁、DD₁的中点，∴BE∥D₁F且BE＝D₁F.

∴四边形BED₁F为平行四边形．

∴D₁E∥BF.

又∵D₁E⊂平面AD₁E，BF⊄平面AD₁E，

∴BF∥平面AD₁E.

又∵G是棱DA的中点，

∴GF∥AD₁.

又∵AD₁⊂平面AD₁E，GF⊄平面AD₁E，

∴GF∥平面AD₁E.

又∵BF∩GF＝F，

∴平面AD₁E∥平面BGF.

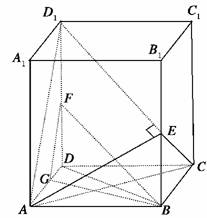
(2)连结CE、AC、BD，∵AA₁＝2，

∴AD₁＝＝，

同理AE＝，D₁E＝.

∴AD＝D₁E²+AE²，

∴D₁E⊥AE.

∵AC⊥BD，AC⊥D₁D，

∴AC⊥平面BB₁D₁D.

又∵D₁E⊂平面BB₁D₁D，

∴AC⊥D₁E.

又∵AC∩AE＝A，AC⊂平面AEC，

AE⊂平面AEC，

∴D₁E⊥平面AEC.

14．如下图所示，已知A₁B₁C₁－ABC是正三棱柱，E、E₁分别是AC、A₁C₁的中点．

(1)求证：平面AB₁E₁∥平面BEC₁；

(2)当该棱柱各棱长都为a时，求(1)中两个平行平面间的距离．

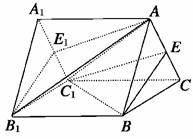
解析：(1)∵E、E₁分别是AC、A₁C₁的中点，

又∵三棱柱为正三棱柱，

⇒平面AB₁E∥平面BEC₁

(2)由(1)可知平面AB₁F与平面BEC₁之间的距离可以转化为A到平面BEC₁的距离，设为d.

∵VC₁－ABE＝VA－BC₁E，

又∵正三棱柱各棱长都是a，

∴AE＝，BE＝a，

∴VC₁－ABE＝····a＝a³，

而BC₁＝a，C₁E＝a，BE＝a，

∴BC＝C₁E²+BE²，

∴∠C₁EB＝90°，

∴S△BC₁E＝·BE·C₁E＝·a·a＝a²，

∴d＝＝＝a，

则(1)中两个平行平面间的距离是a.

13．如图，在四棱锥P－ABCD中，底面ABCD是正方形，侧棱PD⊥底面ABCD，PD＝DC，E是PC的中点，证明PA∥平面EDB.

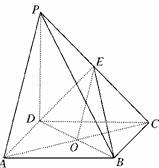
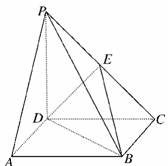
证明：方法一：

连接AC交BD于O.连接EO.

∵底面ABCD是正方形，∴点O是AC的中点．

在△PAC中，EO是中位线，∴PA∥EO.

而EO⊂平面EDB且PA⊄平面EDB，

所以，PA∥平面EDB.

方法二：

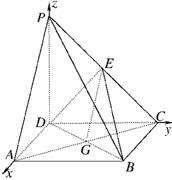如图所示建立空间直角坐标系，D为坐标原点．设DC＝a.

连接AC交BD于G，连接EG.依题意得A(a,0,0)，P(0,0，a)，E(0，，)．

∵底面ABCD是正方形，∴G是此正方形的中心，故点G的坐标为(，，0)，且

＝(a,0，－a)，＝(，0，－)．

∴＝2.这表明PA∥EG.

而EG⊂平面EDB且PA⊄平面EDB，

∴PA∥平面EDB.

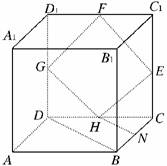
12．如图，在正四棱柱ABCD－A₁B₁C₁D₁中，E、F、G、H分别是棱CC₁、C₁D₁、D₁D、DC的中点，N是BC的中点，点M在四边形EFGH及其内部运动，则M满足条件________时，有MN∥平面B₁BDD₁.

答案：M∈线段FH

解析：因为HN∥BD，HF∥DD₁，所以平面NHF∥平面B₁BDD₁，又平面NHF∩平面EFGH＝FH.故线段FH上任意点M与N相连，有MN∥平面B₁BDD₁，故填M∈线段FH.

11．设平面α∥β，A、C∈α，B、D∈β，直线AB与CD交于S，若AS＝18，BS＝27，CD＝34，则CS＝________.

答案：或68

解析：利用面面平行的性质，通常构造相似三角形求解，但要注意交点S在α、β之间，或在AB、CD的延长线上两种情况，易得CS＝或68.

10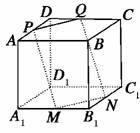．如图所示，ABCD－A₁B₁C₁D₁是棱长为a的正方体，M，N分别是下底面的棱A₁B₁，B₁C₁的中点，P是上底面的棱AD上的一点，AP＝，过P，M，N的平面交上底面于PQ，Q在CD上，则PQ＝________.

答案：a

解析：如图所示，连接AC，

易知MN∥平面ABCD，∴MN∥PQ.

又∵MN∥AC，∴PQ∥AC，

又∵AP＝，∴＝＝＝，

∴PQ＝AC＝a.

9．正方体ABCD－A₁B₁C₁D₁中，E为DD₁的中点，则BD₁与过A、C、E的平面的位置关系是________．

答案：平行

解析：取AC中点F，连结EF，在△BDD₁中，EF∥BD₁，因此，BD₁∥面AEC，平行关系．