8.设函数f(x)=|2x-1|+x+3,则f(-2)=________;若f(x)≤5,则x的取值范围是________.

解析:f(-2)=|-4-1|-2+3=6,

由f(x)≤5,得|2x-1|+x+3≤5,即解集是[-1,1].

答案:6　 [-1,1]

7.(2010·陕西)不等式|x+3|-|x-2|≥3的解集为________.

解析:解法一:当x≤-3时,原不等式可化为-x-3+x-2≥3,即-5≥3,无解.

当-3<x≤2时,原不等式可化为x+3+x-2≥3,即x≥1,∴1≤x≤2.

当x>2时,原不等式可化为x+3-x+2≥3,即5≥3,

∴x>2.

综上,原不等式的解集为{x|x≥1}.

解法二:利用绝对值的几何意义,即求在数轴上到-3点的距离与到2点的距离的差大于等于3,借助数轴可知解集为{x|x≥1}.

答案:{x|x≥1}

6.对任意实数x,若不等式|x+1|-|x-2|>k恒成立,则k的取值范围是(　　 )

A.k<3　　　　　　 　 B.k<-3

C.k≤3　　　　　 　 D.k≤-3

解析:|x+1|-|x-2|的几何意义是数轴上的点x到-1的距离减去x到2的距离所得的差,结合数轴可知该差的最小值为-3,要使不等式|x+1|-|x-2|>k恒成立,只需k<-3即可.故选B.

答案:B

二､填空题:(本大题共4小题,每小题6分,共24分,把正确答案填在题后的横线上.)

5.命题p:“x>1”是“|x|>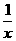”的充要条件;命题q:|x²-8x+16|≤x-4的解集为[4,5],那么(　　 )

A.“p或q”为假　　　　　 　 B.“p且q”为真

C.“p且¬q”为真　　　　　　 D.“¬p且q”为真

解析:|x|>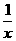⇒x>1或x<0,

∴p假,则¬p真,

又|x²-8x+16|≤x-4,

即-(x-4)≤x²-8x+16≤x-4,

解得4≤x≤5,∴q为真,

∴“¬p且q”为真.

答案:D

4.不等式|2x-log₂x|<2x+|log₂x|成立,则(　　 )

A.1<x<2　　　　　　 B.0<x<1

C.x>1　　　　　　 　 D.x>2

解析:|a+b|≤|a|+|b|中取不等号“<”的条件是“ab<0”.则有x·(-log₂x)<0,又x>0,∴log₂x>0,从而x>1.

答案:C

3.实数x满足log₃x=1+sinθ,则|x-1|+|x-9|的值为(　　 )

A.8　　　　　 　　　 B.-8

C.8或-8　　　　　　 D.与θ有关

解析:由sinθ∈[-1,1]得1≤x≤9,

∴|x-1|+|x-9|=8.

答案:A

2.已知实数a,b,c满足|a-c|<|b|,则下列不等式成立的是(　　 )

A.a<b+c　　　　　　 B.|a|>|b|-|c|

C.a<c-b　　　　　　 D.|a|<|b|+|c|

解析:由已知-|b|<a-c<|b|,

∴c-|b|<a<|b|+c≤|b|+|c|,

∴|a|<|b|+|c|.

答案:D

1.“|x-a|<m,且|y-a|<m”是“|x-y|<2m”(x,y,a,m∈R)的(　　 )

A.充分非必要条件

B.必要非充分条件

C.充要条件

D.非充分非必要条件

分析:利用绝对值三角不等式,推证

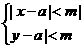
与|x-y|<2m的关系即得答案.

解析:∵|x-y|=|(x-a)-(y-a)|≤|x-a|+|y-a|<m+m=2m,

∴|x-a|<m,且|y-a|<m是|x-y|<2m的充分条件.

取x=3,y=1,a=-2,m=2.5,则有

|x-y|=2<5=2m,但|x-a|=5,

不满足|x-a|<m=2.5,

故|x-a|<m且|y-a|<m不是|x-y|<2m的必要条件.

答案:A

13．已知函数f(x)＝log_a(3－ax)．

(1)当x∈[0,2]时，函数f(x)恒有意义，求实数a的取值范围；

(2)是否存在这样的实数a，使得函数f(x)在区间[1,2]上为减函数，并且最大值为1？如果存在，试求出a的值；如果不存在，请说明理由．

解：(1)由题设，3－ax>0对一切x∈[0,2]恒成立，

a>0且a≠1，

∵a>0，∴g(x)＝3－ax在[0,2]上为减函数，

从而g(2)＝3－2a>0，∴a<，

∴a的取值范围为(0,1)∪.

(2)假设存在这样的实数a，由题设知f(1)＝1，

即log_a(3－a)＝1，∴a＝，

此时f(x)＝log(3－x)，

当x＝2时，f(x)没有意义，故这样的实数不存在．

评析：这是一道探索性问题，注意函数、方程、不等式之间的相互转化，存在性问题的处理，一般是先假设存在，再结合已知条件进行转化求解，如推出矛盾，则不存在，反之，存在性成立．

12．已知a>0，a≠1，f(log_ax)＝.试判断f(x)在定义域上是否为单调函数？若是，是增函数还是减函数？若不是，请说明理由．

解：用换元法求出f(x)的解析式，由于其中含有字母，故需讨论．

设t＝log_ax，则x＝a^t，

∵f(t)＝·　即f(t)＝(a^t－a^－t)．

∴f(x)＝(a^x－a^－x)．

f(x)的定义域是(－∞，+∞)，设x₁<x₂，则

f(x₁)－f(x₂)＝[(ax₁－a－x₁)－(ax₂－a－x₂)]

＝·.

∵a>0，a≠1，∴ax₁ax₂>0,1+ax₁ax₂>0.

若0<a<1，则ax₁>ax₂，ax₁－ax₂>0.

此时<0，

∴f(x₁)－f(x₂)<0，即f(x₁)<f(x₂)．

同理若a>1，f(x₁)<f(x₂)．

综上所述，当a>0且a≠1时，f(x)在(－∞，+∞)上是单调函数，是单调增函数．

评析：对于y＝a^x，由于其单调性与a的取值有关，故需分0<a<1和a>1两种情况讨论．