1、把握直线与圆的位置关系的三种常见题型：

①相切--求切线

②相交--求距离

③相离--求圆上动点到直线距离的最大(小)值；

问题1：直线与圆相切，则实数等于　　　　 　

[解析]圆心为，半径为，或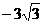

4.圆系方程

①以点为圆心的圆系方程为

②过圆和直线的交点的圆系方程为

③过两圆，的交点的圆系方程为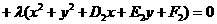(不表示圆)

★重难点突破★

重点:根据给定的方程判定直线与圆、圆与圆的位置关系；

　　 利用直线和圆、圆与圆的位置关系的充要条件解决一些简单的问题；

难点:借助数形结合,利用圆的几何性质,将题目所给条件转化为圆心到直线的距离、两圆的连心线或半径的和与差

重难点:将方程的理论与圆的几何性质相结合,并加以运用

3. 相切问题的解法：

①利用圆心到切线的距离等于半径列方程求解

②利用圆心、切点连线的斜率与切线的斜率的乘积为-1

③利用直线与圆的方程联立的方程组的解只有一个，即来求解。

特殊地,已知切点,圆的切线方程为,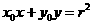

圆的切线方程为

2.两圆的的位置关系

　(1)设两圆半径分别为，圆心距为d

　若两圆相外离，则　 ，公切线条数为4

　若两圆相外切,则，公切线条数为3

　若两圆相交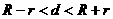，则，公切线条数为2

若两圆内切，则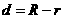，公切线条数为1

若两圆内含，则，公切线条数为0

(2) 设两圆，，若两圆相交，则两圆的公共弦所在的直线方程是

1.判断直线与圆的位置关系有两种方法：

①几何法：通过圆心到直线的距离与半径的大小比较来判断，设圆心到直线的距离为，圆半径为，若直线与圆相离，则；若直线与圆相切，则；若直线与圆相交，则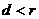 ②代数法：通过直线与圆的方程联立的方程组的解的个数来判断，即通过判别式来判断，若，则直线与圆相离；若，则直线与圆相切；若，则直线与圆相交

13.(2010·江门二模)已知函数f(x)=x|x-a|,a∈R是常数.

(1)若a=1,求y=f(x)在点P(-1,f(-1))处的切线;

(2)是否存在常数a,使f(x)<2x+1对任意x∈(-∞,2)恒成立?若存在,求常数a的取值范围;若不存在,简要说明理由.

解:(1)当a=1时,f(x)=x|x-1|=

在点P(-1,f(-1))附近,f(x)=x-x²,

因此f′(x)=1-2x,

故f′(-1)=3,

因此P(-1,-2)处的切线方程为y+2=3(x+1),

即3x-y+1=0.

(2)存在,f(x)<2x+1,即x|x-a|<2x+1,(*)

当x=0时,(*)等价于0<1,对任意a∈R恒成立.

当0<x<2时,(*)等价于|x-a|<2+,

即x-2- <a<2+x+,

由于2+x+≥4,等号当且仅当x=1时成立,

由于

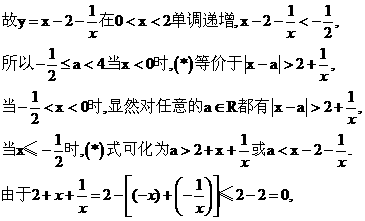
等号当且仅当-x=1,

即x=-1时成立,

所以a>0,

由于y=x-2-在x<0的取值范围为R,

所以a<x-2-恒成立的a的解集为空集.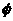

所以,常数a的取值范围为

12.(2010·全国新课标)设函数f(x)=|2x-4|+1.

(1)画出函数y=f(x)的图象;

(2)若不等式f(x)≤ax的解集非空,求a的取值范围.

解:(1)由于f(x)=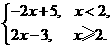

则函数y=f(x)的图象如图所示.

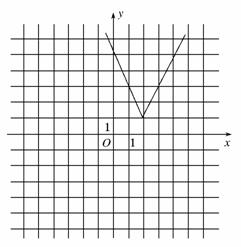
(2)由函数y=f(x)与函数y=ax的图象可知(l₁,l₂,l₃,l₄都代表y=ax的图象),l₁与y=f(x)相交于点A,由l₁转到l₂时有交点,

∴a≥y.

同理当l₁转到l₃时也有交点,当转到l₄时,此时l₄与y=-2x+5平行无交点,

∴a<-2.

故不等式f(x)≤ax的解集非空时,a的取值范围为(-∞,-2)∪.

评析:本题主要考查分段函数画图和利用数形结合找出a的取值范围.

11.(2010·福建)已知函数f(x)=|x-a|.

(1)若不等式f(x)≤3的解集为{x|-1≤x≤5},求实数a的值;

(2)在(1)的条件下,若f(x)+f(x+5)≥m对一切实数x恒成立,求实数m的取值范围.

解:(1)由f(x)≤3得|x-a|≤3,

解得a-3≤x≤a+3.

又已知不等式f(x)≤3的解集为{x|-1≤x≤5},

所以

解得a=2.

(2)解法一;当a=2时,f(x)=|x-2|.

设g(x)=f(x)+f(x+5),

于是g(x)=|x-2|+|x+3|=

所以当x<-3时,g(x)>5;

当-3≤x≤2时,g(x)=5;

当x>2时,g(x)>5.

综上可得,g(x)的最小值为5.

从而,若f(x)+f(x+5)≥m,即g(x)≥m对一切实数x恒成立,则m的取值范围为(-∞,5].

解法二:当a=2时,f(x)=|x-2|.

设g(x)=f(x)+f(x+5).

由|x-2|+|x+3|≥|(x-2)-(x+3)|=5(当且仅当-3≤x≤2时等号成立)得,g(x)的最小值为5.

从而,若f(x)+f(x+5)≥m,即g(x)≥m,对一切实数x恒成立,则m的取值范围为(-∞,5].

评析:对于绝对值不等式,去绝对值是关键.要掌握好下列几种方法:①定义法,②平方法,③不等式法.根据不同情况灵活选择.

10.若不等式|3x-b|<4的解集中整数有且仅有1,2,3,则实数b的取值范围是________.

解析:不等式|3x-b|<4⇔-4<3x-b<4,

∴.　　 (*)

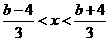若原不等式的整数解只有1,2,3,

由(*)式,知0≤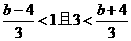≤4,

解之得4≤b<7且5<b≤8,∴5<b<7.

答案:5<b<7

三､解答题:(本大题共3小题,11､12题13分,13题14分,写出证明过程或推演步骤.)

9.以下三个命题:①若|a-b|<1,则|a|<|b|+1;②若a､b∈R,则|a+b|-2|a|≤|a-b|;③若|x|<2,|y|>3,则|,其中正确命题的序号是________.

解析:①|a|-|b|≤|a-b|<1,所以|a|<|b|+1;

②|a+b|-|a-b|≤|(a+b)+(a-b)|=|2a|,

所以|a+b|-2|a|≤|a-b|;

③|x|<2,|y|>3,所以,

所以.故三个命题都正确.

答案:①②③