
题目列表(包括答案和解析)
3.已知正三角形 的三个顶点都在抛物线
的三个顶点都在抛物线 上,其中
上,其中 为坐标原点, 求
为坐标原点, 求 的内接圆的方程;
的内接圆的方程;
解法一:设 两点坐标分别为
两点坐标分别为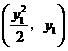 ,
, ,由题设知
,由题设知
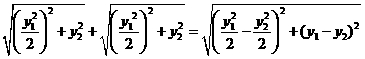

解得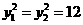 ,
,
所以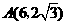 ,
,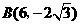 或
或 ,
,

设圆心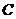 的坐标为
的坐标为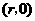 ,则
,则 ,所以圆
,所以圆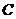 的方程为
的方程为
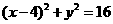

解法二:设 两点坐标分别为
两点坐标分别为 ,
, ,由题设知
,由题设知


又因为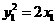 ,
,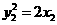 ,可得
,可得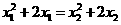
 即
即
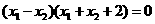

由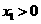 ,
, ,可知
,可知 ,故
,故 两点关于
两点关于 轴对称,所以圆心
轴对称,所以圆心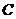 在
在 轴上
轴上
设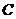 点的坐标为
点的坐标为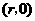 ,则
,则 点坐标为
点坐标为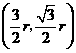 ,于是有
,于是有 ,解得
,解得 ,所以圆
,所以圆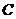 的方程为
的方程为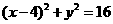

2. (山东省德州市2008届高中三年级教学质量检测)
如图所示,过圆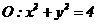 与
与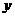 轴正半轴的交点A作圆的切线
轴正半轴的交点A作圆的切线 ,M为
,M为 上任意一点,再过M作圆的另一切线,切点为Q,当点M在直线
上任意一点,再过M作圆的另一切线,切点为Q,当点M在直线 上移动时,求三角形MAQ的垂心的轨迹方程.
上移动时,求三角形MAQ的垂心的轨迹方程.

[解析]设 边上的高为
边上的高为 边上的高为
边上的高为 ,连接
,连接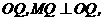
当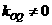 时,
时, ………………4′
………………4′
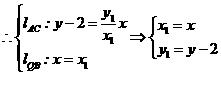 ………………8′
………………8′
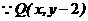 在
在 上
上
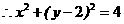 ………………10′
………………10′
当 时,此时垂心为点B,也满足方程.
时,此时垂心为点B,也满足方程.
而点M与点N重合时,不能使A,M,Q构成三角形,故 的垂心的轨迹方程为
的垂心的轨迹方程为
 ………………12′
………………12′
1. (华南师大附中2007-2008学年第一学期高三期末水平测试)
已知直线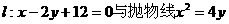 交于A、B两点,过A、B两点的圆与抛物线在A(其中A点在y轴的右侧)处有共同的切线.
交于A、B两点,过A、B两点的圆与抛物线在A(其中A点在y轴的右侧)处有共同的切线.
(1)求圆M的方程;
(2)若圆M与直线y=mx交于P、Q两点,O为坐标原点,求证: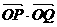 为定值.
为定值.
[解析](1)由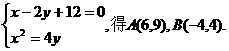
抛物线在A处的切线斜率为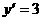 ,设圆的方程为
,设圆的方程为 ,
,
由切线性质得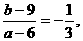 ①
①
又圆心在AB的中垂线上,即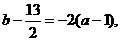 ②
②
由①②得圆心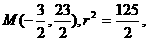
圆M的方程为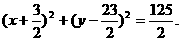
(2)由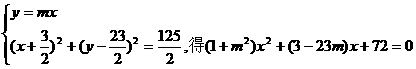
设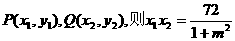 ,
,
又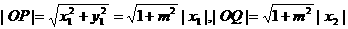 ,
, 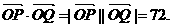
10、 (08江苏泰州联考)如图,已知圆心坐标为
(08江苏泰州联考)如图,已知圆心坐标为 的圆
的圆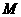 与
与 轴及直线
轴及直线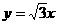 分别相切于
分别相切于 、
、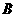 两点,另一圆
两点,另一圆 与圆
与圆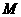 外切、且与
外切、且与 轴及直线
轴及直线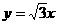 分别相切于
分别相切于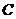 、
、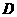 两点.
两点.
(1)求圆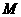 和圆
和圆 的方程;
的方程;
(2)过点B作直线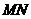 的平行线
的平行线 ,求直线
,求直线 被圆
被圆 截得的弦的长度.
截得的弦的长度.
[解析](1)由于⊙M与∠BOA的两边均相切,故M到OA及OB的距离均为⊙M的半
径,则M在∠BOA的平分线上,同理,N也在∠BOA的平分线上,
即O,M,N三点共线,且OMN为∠BOA的平分线,
∵M的坐标为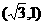 ,∴M到
,∴M到 轴的距离为1,即⊙M的半径为1,
轴的距离为1,即⊙M的半径为1,
则⊙M的方程为 ,
,
设⊙N的半径为 ,其与
,其与 轴的的切点为C,连接MA、MC,
轴的的切点为C,连接MA、MC,
由Rt△OAM∽Rt△OCN可知,OM:ON=MA:NC,
即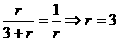 ,
,
则OC= ,则⊙N的方程为
,则⊙N的方程为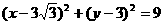 ;
;
(2)由对称性可知,所求的弦长等于过A点直线MN的平行线被⊙ 截得的弦的长度,此弦的方程是
截得的弦的长度,此弦的方程是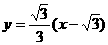 ,即:
,即: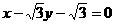 ,
,
圆心N到该直线的距离d=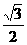 ,
,
则弦长= .
.
参考例题:
9、直线 与抛物线
与抛物线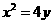 交于
交于 两点,过
两点,过 两点的圆
两点的圆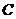 与抛物线在点
与抛物线在点 处有共同的切线,求圆
处有共同的切线,求圆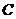 的方程
的方程
[解析]由 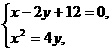 得点
得点 的坐标分别是(6,9)、(-4,4),
的坐标分别是(6,9)、(-4,4),
由 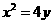 得
得 
所以抛物线 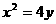 在点
在点 处切线的斜率为
处切线的斜率为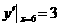 ,
,
设圆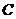 的圆心为
的圆心为 , 方程是
, 方程是
则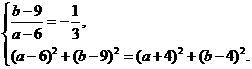 解得
解得 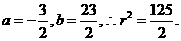
则圆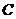 的方程是
的方程是 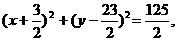 (或
(或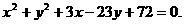
8、已知点A(–2,0),B(2,0),曲线C上的动点P满足 ,
,
(1)求曲线C的方程;
(2)若过定点M(0,–2)的直线l与曲线C有交点,求直线l的斜率k的取值范围;
(3)若动点Q(x,y)在曲线C上,求 的取值范围.
的取值范围.
[解析](1)设P(x,y), ,得
,得
P点轨迹(曲线C)方程为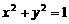 ,即曲线C是圆.
,即曲线C是圆.
(2)可设直线l方程为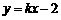 ,其一般方程为:
,其一般方程为: ,…6分
,…6分
由直线l与曲线C有交点,得
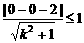 ,
,
得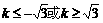 ,
,
即所求k的取值范围是 ;
;
(3)由动点Q(x,y),设定点M(0,–2),
则直线QM的斜率为: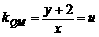 ,
,
又点Q在曲线C上,故直线QM与圆有交点,由(2)结论,得
kQM的取值范围是 ,
,
∴u的取值范围是 .
.
7、过圆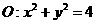 外一点
外一点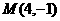 引圆的两条切线,则经过两切点的直线方程为
引圆的两条切线,则经过两切点的直线方程为
A. B.
B. 
C. 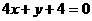 D.
D.

[解析]A.
以线段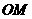 为直径的圆的方程为
为直径的圆的方程为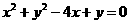 ,经过两切点的直线就是两圆的公共弦所在的直线,将两圆的方程相减得
,经过两切点的直线就是两圆的公共弦所在的直线,将两圆的方程相减得 ,这就是经过两切点的直线方程
,这就是经过两切点的直线方程
6、方程ax2+ay2-4(a-1)x+4y=0表示圆,求a的取值范围,并求出其中半径最小的圆的方程.
[解析](1)∵a≠0时,方程为[x-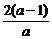 ]2+(y+
]2+(y+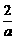 )2=
)2=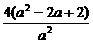 ,
,
由于a2-2a+2>0恒成立,
∴a≠0且a∈R时方程表示圆.
(2)r2=4·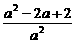 =4[2(
=4[2(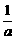 -
- )2+
)2+ ],
],
∴a=2时,rmin2=2.
此时圆的方程为(x-1)2+(y-1)2=2.
综合提高训练
5、已知圆C1: 相交于A,B两点,则线段AB的中垂线方程为
。
相交于A,B两点,则线段AB的中垂线方程为
。
[解析] x+y-3=0 [即两圆的连心线]
4、直线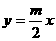 与圆
与圆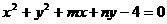 交于
交于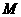 、
、 两点,且
两点,且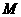 、
、 关于直线
关于直线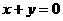 对称,则弦
对称,则弦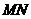 的长为
的长为
[解析] 4
由直线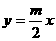 与直线
与直线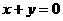 垂直得m=2,由圆心在直线
垂直得m=2,由圆心在直线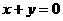 上得n=-2;
上得n=-2;
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com