
题目列表(包括答案和解析)
2、已知三条直线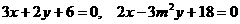 和
和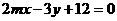 围成一个直角三角形,则
围成一个直角三角形,则 的值是
的值是
A. 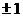 或
或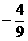 B.-1或
B.-1或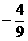 C.0或-1或
C.0或-1或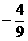 D.0或
D.0或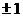 或
或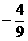
[解析] C[直线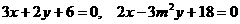 垂直时,
垂直时, ,但
,但 时后两条直线重合,又
时后两条直线重合,又 时后两条直线垂直,故选C]
时后两条直线垂直,故选C]
1、若过点 和
和 的直线与直线
的直线与直线 平行,则
平行,则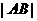 的值为
的值为
A.6
B. C.2 D.
C.2 D.
[解析] ,
,
12.直线 经过直线
经过直线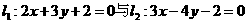 的交点,且与坐标轴围成的三角形是等腰直角三角形,求直线
的交点,且与坐标轴围成的三角形是等腰直角三角形,求直线 的方程
的方程
解析:设直线 方程为
方程为
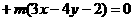 ,
,
化简得:
 直线
直线 与坐标轴围成的三角形是等腰直角三角形,
与坐标轴围成的三角形是等腰直角三角形, 直线
直线 的斜率为
的斜率为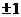
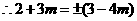 ,解得:
,解得: 或
或
代入并化简得直线 的方程为
的方程为 或
或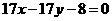
★抢分频道★
基础巩固训练
11.已知为m实数,直线 :(2m+1)x+(1-m)y-(4m+5)=0, P(7,0),求点P到直线
:(2m+1)x+(1-m)y-(4m+5)=0, P(7,0),求点P到直线 的距离d的取值范围。
的距离d的取值范围。
[解析] 直线 过定点
过定点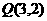 ,d的最大值为点P、Q的距离,因点P、Q的距离为
,d的最大值为点P、Q的距离,因点P、Q的距离为 ,故d的取值范围是
,故d的取值范围是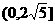
10、方程 所确定的直线必经过点
所确定的直线必经过点
A.(2,2) B.(-2,2) C.(-6,2) D.(3,-6)
[解析]代入验证,选A
9.求过原点且与两定点 距离相等的直线
距离相等的直线 的方程
的方程
[解析] 直线 过线段AB的中点或平行于直线AB,故方程为
过线段AB的中点或平行于直线AB,故方程为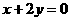 或
或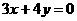
考点3 直线系
题型1:运用直线系求直线方程
[例5 ]求过直线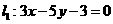 和
和 的交点,且与直线
的交点,且与直线 垂直的直线方程和平行的直线方程。
垂直的直线方程和平行的直线方程。
[解题思路]可直接求交点,也可用直线系求解
[解析]解法一.设与直线 垂直的直线方程为
垂直的直线方程为
设与直线 平行的直线方程为
平行的直线方程为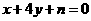 联立方程得
联立方程得 与
与 的交点(1,-1)
代入求得 m=-5,n=3
的交点(1,-1)
代入求得 m=-5,n=3
解法二.设与直线为 由条件分别求得
由条件分别求得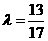 和
和 化简得
化简得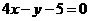 和
和
[名师指引](1)使用直线系方程可以回避解方程组,从而达到减少运算量的目的
(2)注意直线系 不表示直线
不表示直线 ,这是一个容易丢解的地方
,这是一个容易丢解的地方
题型2:动直线过定点问题
[例6 ]已知圆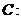

 ,直线
,直线
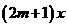
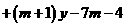
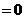
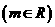 ⑴证明不取何值,直线
⑴证明不取何值,直线 过定点 ⑵证明直线
过定点 ⑵证明直线 恒与圆C相交
恒与圆C相交
[解析](1)直线化为: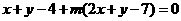 故直线是经过
故直线是经过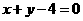 和
和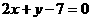 交点(3,1)的直线系,故过定点(3,1)
交点(3,1)的直线系,故过定点(3,1)
(2)因为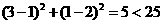 所以(3,1)为圆内的点。故直线
所以(3,1)为圆内的点。故直线 恒与圆C相交
恒与圆C相交
[名师指引]在处理动直线过定点问题时,分离参数,转化为过两条定直线的交点的直线系是简单易行的方法
[新题导练]
8. 两平行直线 ,
, 分别过点P(-1,3),Q(2,-1)它们分别绕P,Q旋转,但始终保持平行,则之
分别过点P(-1,3),Q(2,-1)它们分别绕P,Q旋转,但始终保持平行,则之 ,
, 间的距离的取值范围是( )
间的距离的取值范围是( )
A. B.(0,5)
C.
B.(0,5)
C.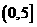 D.
D.
[解析]最大值为P,Q的距离,即5,选C
7. 与直线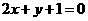 的距离为
的距离为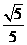 的直线方程为
的直线方程为
[解析]  或
或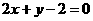
6. 点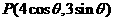 到直线
到直线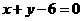 的距离的最小值等于
的距离的最小值等于
[解析]
4. (山东省枣庄市2008届高三第一次调研考试)
已知直线l的倾斜角为 ,直线l1经过点
,直线l1经过点 垂直,直线l2:
垂直,直线l2:
|
 等于 (
)
等于 (
)
A.-4 B.-2 C.0 D.2
[解析] B [ ,又
,又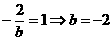 ]
]
考点2 点到直线的距离
题型:利用两个距离公式解决有关问题
[例3 ] 已知直线 及点
及点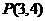
(1)证明直线 过某定点,并求该定点的坐标
过某定点,并求该定点的坐标
(2)当点 到直线
到直线 的距离最大时,求直线
的距离最大时,求直线 的方程
的方程
[解题思路]分离参数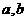 求定点坐标;寻找
求定点坐标;寻找 到直线
到直线 的距离最大时,直线
的距离最大时,直线 满足的条件
满足的条件
解析:(1)将直线 的方程化为:
的方程化为: ,
,
 无论
无论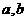 如何变化,该直线系都恒过直线
如何变化,该直线系都恒过直线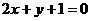 与直线
与直线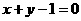 的交点,
的交点,
由 得
得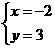 ,
, 直线
直线 过定点
过定点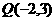
(2)当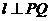 时点
时点 到直线
到直线 的距离最大,此时直线
的距离最大,此时直线 的斜率为-5,
的斜率为-5, 直线
直线 的方程为
的方程为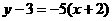 即
即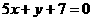
[名师指引](1)斜率不定的动直线,都应考虑是否过定点
(2)处理解析几何的最值问题,一般方法有:函数法;几何法
[例4 ] 已知三条直线

 ,若
,若 与
与 的距离是
的距离是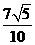
(1)求a的值
(2)能否找到一点P使得P同时满足下列三个条件①P是第一象限的点;②P点到 的距离是P点到
的距离是P点到 的距离的
的距离的 ③P点到
③P点到 的距离与P点到
的距离与P点到 的距离的之比是
的距离的之比是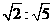 ;若能,求P点坐标;若不能,说明理由。
;若能,求P点坐标;若不能,说明理由。
[解题思路]由三个条件可列三个方程或不等式,最终归结为混合组是否有解的问题
[解析](1)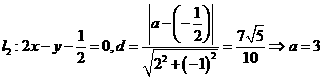
(2)设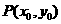 同时满足三个条件
同时满足三个条件
由②得:设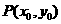 在
在 上
上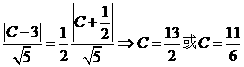
则有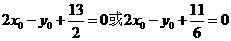 ------------(1)
------------(1)
由③得:
 --------------(2)
--------------(2)
由①得  ----------------(3)
----------------(3)
解由(1)(2)(3)联立的混合组得  所以
所以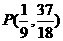
[名师指引](1)在条件比较多时,思路要理顺;(2)解混合组时,一般是先解方程,再验证不等式成立
[新题导练]
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com