
题目列表(包括答案和解析)
8.已知直线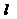 经过点
经过点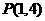 ,分别交
,分别交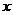 轴,
轴,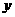 轴正半轴于点A,B,其中O为原点,求
轴正半轴于点A,B,其中O为原点,求
△AOB的面积最小时,直线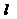 的方程;
的方程;
[解析]
设直线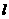 的方程为
的方程为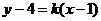 ,
,
令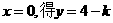 ,令
,令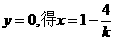 ,
,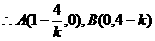 ,
,

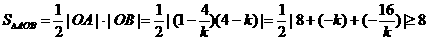 ,
,
当且仅当 ,即k=±4时等号成立,但k<0,故直线
,即k=±4时等号成立,但k<0,故直线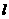 的方程为:
的方程为: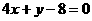
考点3 对称问题
题型1:求点关于某直线的对称点或求两点的对称直线方程
[例5 ] [例5 ]已知直线l:2x-3y+1=0,点A(-1,-2),求:
(1)点A关于直线l的对称点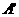 的坐标;
的坐标;
(2)直线m:3x-2y-6=0关于直线l的对称直线 方程;
方程;
(3)直线l关于点A(-1,-2)对称的直线 的方程;
的方程;
[解题思路]:求对称直线的方程,方法1是转化为点对称问题,二是用相关点转移法解决;
[解析](1)设点A关于l的对称点是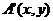 ,
,
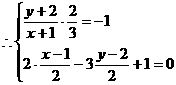
解得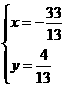
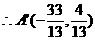
(2)设点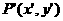 是直线m上任意一点,
是直线m上任意一点,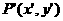 关于直线
关于直线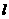 的对称点为
的对称点为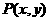
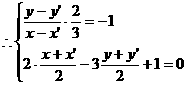 解得:
解得: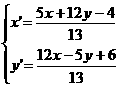
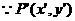 在直线
在直线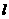 上,
上, 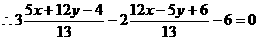
化简得: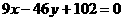
(3)设点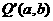 是直线
是直线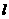 上任意一点,点
上任意一点,点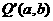 关于点A(-1,-2)的对称点为
关于点A(-1,-2)的对称点为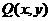 ,
,
则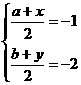 ,解得
,解得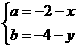
因点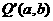 在直线
在直线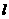 上,
上,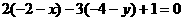 ,
,
化简得: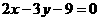
[名师指引](1)要抓住两点关于直线对称的特征来列式;
(2)点对称是其它对称问题(曲线的对称等)的基础,务必重点掌握;
题型2:利用对称知识解决有关问题
[例6 ] [2008·深一模] 如图,已知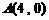 、
、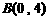 ,从点
,从点 射出的光线经直线
射出的光线经直线 反向后再射到直线
反向后再射到直线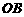 上,最后经直线
上,最后经直线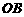 反射后又回到
反射后又回到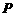 点,则光线所经过的路程是 A.
点,则光线所经过的路程是 A.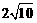 B.
B.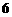 C.
C.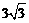 D.
D.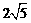


[解题思路]:利用对称知识,将折线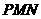 的长度转化为折线
的长度转化为折线 的长度
的长度
[解析] 设点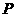 关于直线
关于直线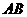 的对称点为
的对称点为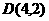 ,关于
,关于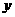 轴的对称点为
轴的对称点为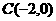 ,则光线所经过的路程
,则光线所经过的路程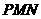 的长
的长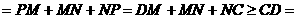
[名师指引]本例是运用数形结合解题的典范,关键是灵活利用平面几何知识与对称的性质实现转化,一般地,在已知直线上求一点到两个定点的距离之和的最小值,需利用对称将两条折线由同侧化为异侧,在已知直线上求一点到两个定点的距离之差的最大值,需利用对称,将两条折线由异侧化为同侧,从而实现转化。
[新题导练]
7.已知点A(3,4)
(1)经过点A且在两坐标轴上截距相等的直线方程为: ;
(2)经过点A且与两坐标轴围成的三角形面积是1的直线方程为 :
(3)经过点A且与两坐标轴围成一个等腰直角三角形的直线方程为: ;
(4)经过点A且在x轴上的截距是在y轴上的截距的2倍的直线方程为: ;
[解析](1)4x-3y=0或x+y-7=0
[当直线经过原点时,方程为4x-3y=0,当直线不经过原点时,设方程为 ,代入点A的坐标得直线方程x+y-7=0]
,代入点A的坐标得直线方程x+y-7=0]
(2)2x-y-2=0或8x-9y+12=0;[设直线方程为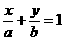 ,由
,由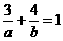 和
和 求得
求得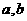 的值]
的值]
(3)x-y+1=0或x+y-7=0;[斜率为1或-1,由点斜式易得]
(4)x+2y-11=0或4x-3y=0;[当直线经过原点时,方程为4x-3y=0,当直线不经过原点时,设直线方程为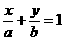 ,由
,由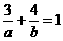 和
和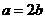 求得
求得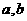 的值]
的值]
6.已知点A(-2,3),B(3,2),P(0,-2),过P点的直线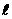 与线段AB有公共点,求直线
与线段AB有公共点,求直线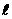 的斜率k的变化范围;
的斜率k的变化范围;
[解析] 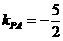 ,
,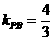 ,画出图形,数形结合可得结果
,画出图形,数形结合可得结果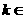
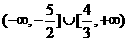
考点2 求直线方程
题型:根据题目条件,选择方程的形式求直线方程
[例3 ] 等腰直角三角形ABC的直角顶点C和顶点B都在直线2x+y–6=0上,顶点A的坐标是(1, –1),求边AB, AC所在的直线方程.
[解题思路]从确定直线AB, AC 的条件入手,直线AC满足:经过点A且垂直于直线2x+y–6=0,
直线AB满足:经过点A且与直线2x+y–6=0成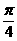 角,(或|AB|等于点A到直线2x+y–6=0的距离的
角,(或|AB|等于点A到直线2x+y–6=0的距离的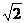 倍)
倍)
解法1:由条件知直线AC垂直于直线2x+y–6=0,设直线AC的方程为x-2y+c=0,
把A(1, –1)代入得c=-3, 故直线AC的方程为x-2y-3=0,
 ,设B(x,y),则
,设B(x,y),则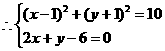 ,
,
解得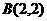 或
或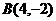 ,所以直线AB的方程为
,所以直线AB的方程为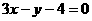 或
或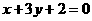
解法2: 直线AC的斜率为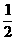 ,由点斜式并化简得,直线AC的方程为x-2y-3=0
,由点斜式并化简得,直线AC的方程为x-2y-3=0
考虑直线AB, AC的夹角为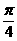 ,设直线AB, AC的方向向量分别为
,设直线AB, AC的方向向量分别为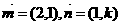
则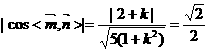 ,解得
,解得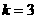 或
或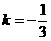 ,所以直线AB的方程为
,所以直线AB的方程为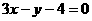 或
或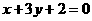
[名师指引]求直线方程的一般步骤:(1)寻找所求直线的满足的两个条件(2)将条件转化,使转化后的条件更利于列出方程组(3)列方程组求解
[例4] 过点P(0,1)作直线l,使它被两直线l1:2x+y-8=0和l2:x-3y+10=0所截得的线段被点P平分的直线的方程.
[解题思路1]:设出直线l的点斜式方程,分别与直线l1,l2建立方程组,求出交点坐标,再用中点坐标公式求出k,即可求出l的方程;
解析1:由题意可知直线l的斜率存在,设直线l的方程为y=kx+1
联立 解得交点坐标是
解得交点坐标是
联立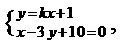 解得交点坐标是
解得交点坐标是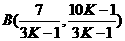
而点P(0,1)是AB的中点,∴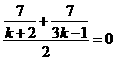 ,解得k=-
,解得k=- ,
,
故所求的直线方程为: x+4y-4=0;
[解题思路2]:设出l,l1的交点A坐标(x1,y1),通过中点坐标公式求出l与l2的交点B的坐标,然后分别将A,B两点的坐标带入直线l1, l2的方程,联立方程组进行求解;
解析2:设直线l与已知l1, l2的交点A(x1,y1),B(x2,y2)
∵P是AB的中点
∴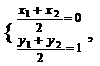 即
即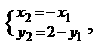 带入l2的方程的,
带入l2的方程的,
得(-x1)-3(2-y1)+10=0,即x1-3y1-4=0
联立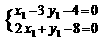 解得A(4,0)
解得A(4,0)
故所求的直线方程为: ,即x+4y-4=0.
,即x+4y-4=0.
[名师指引](1)解法1思路明显,但运算量较大,解法2使用“设而不求” 减少了运算量
(2)中点弦问题和两条曲线关于某点对称的问题,都可以考虑运用解法2中的“设而不求”
[新题导练]
5.在平面直角坐标系中,点 的坐标分别为
的坐标分别为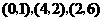 .如果
.如果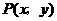 是
是 围成的区域(含边界)上的点,则
围成的区域(含边界)上的点,则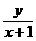 的取值范围是
的取值范围是
[解析] :把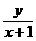 看作区域上的点与点(-1,0)连线的斜率,结合图形可得结果为
看作区域上的点与点(-1,0)连线的斜率,结合图形可得结果为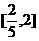
4. 若 为不等式组
为不等式组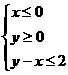 表示的平面区域,则当
表示的平面区域,则当 从-2
从-2
连续变化到1时,动直线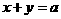 扫过
扫过 中的那部分区域的面积为
中的那部分区域的面积为
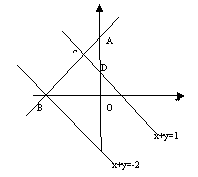
[解析] 如图,当 从-2连续变化到1时,动直线
从-2连续变化到1时,动直线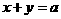 扫过
扫过 中的那部分(四边形OBCD)区域的面积与区域A(
中的那部分(四边形OBCD)区域的面积与区域A(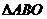 )的面积之比为
)的面积之比为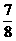 ,而区域A的面积为2,故所求的面积为
,而区域A的面积为2,故所求的面积为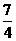
3. (华南师大附中2009届高三综合测试(一))已知直线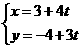 (t为参数),则下列说法错误的是 ( )
(t为参数),则下列说法错误的是 ( )
A.直线的倾斜角为 B.直线必经过点
B.直线必经过点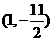
C.直线不经过第二象限 D.当t=1时,直线上对应点到点(1,2)的距离为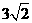
 [解析]D. 将直线方程化为
[解析]D. 将直线方程化为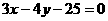 ,直线的斜率为
,直线的斜率为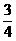 ,直线的倾斜角为
,直线的倾斜角为 ,将点
,将点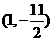 代入,满足方程,斜率为正,截距为负,直线不经过第二象限
代入,满足方程,斜率为正,截距为负,直线不经过第二象限
2.(广东省四校联合体2007-2008学年度联合考试)若函数f(x)=log2(x+1)且a>b>c>0,则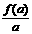 、
、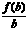 、
、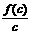 的大小关系是
的大小关系是
A、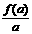 >
>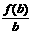 >
>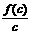 B、
B、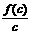 >
>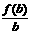 >
>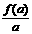
C、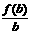 >
> >
>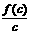 D、
D、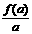 >
>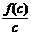 >
>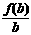
[解析]B
把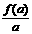 、
、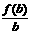 、
、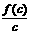 分别看作函数f(x)=log2(x+1)图像上的点
分别看作函数f(x)=log2(x+1)图像上的点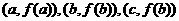 与原点连线的斜率,对照草图可得答案
与原点连线的斜率,对照草图可得答案
1. 下列多组点中,三点共线的是( )
A.(1,4),(-1,2),(3,5) B.(-2,-5),(7,6),(-5,3)
C.(1,0),(0,-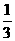 ),(7,2) D.(0,0),(2,4),(-1,3)
),(7,2) D.(0,0),(2,4),(-1,3)
[解析]C. 由KAB=KBC可得
3.几种特殊直线的方程:
①过点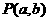 垂直于x轴的直线方程为x=a;过
垂直于x轴的直线方程为x=a;过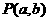 垂直于y轴的直线方程为y=b
垂直于y轴的直线方程为y=b
②已知直线的纵截距为 ,可设其方程为
,可设其方程为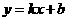 ;
;
③已知直线的横截距为 ,可设其方程为
,可设其方程为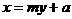 ;
;
④过原点的直线且斜率是k的直线方程为y=kx
★重难点突破★
重点: 理解倾斜角与斜率的对应关系,熟练利用五种形式求直线方程
难点:在求直线方程时,条件的转化和设而不求的运用
重难点:结合图形,把已知条件转化为确定直线位置的要素,从而顺利求出直线方程
(1)倾斜角与斜率的对应关系
涉及这类问题的题型一般有:(1)已知倾斜角(或范围)求斜率(范围)(2)已知斜率(或范围)求倾斜角(或范围),如:
问题1:直线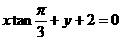 的倾斜角
的倾斜角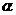 是
是
A.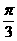 B.
B. 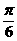 C.
C. 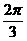 D.
D. 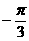
点拨:转化为: 已知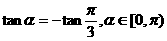 ,求
,求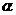 ,答案: C
,答案: C
问题2: 求直线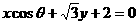 的倾斜角的取值范围
的倾斜角的取值范围
点拨: 要从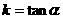 和正切函数的单调性来理解倾斜角与斜率的对应关系,
和正切函数的单调性来理解倾斜角与斜率的对应关系,
①当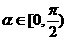 时,
时,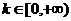 ,
,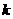 随
随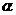 的增大而增大;
的增大而增大;
②当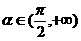 时,
时,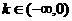 ,
,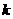 随
随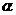 的增大而增大.
的增大而增大.
本题可先求出斜率的取值范围,再利用倾斜角与斜率的对应关系,求出倾斜角的取值范围.
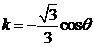 ,故:
,故: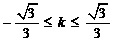
当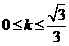 时,直线的倾斜角α满足:
时,直线的倾斜角α满足: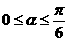
当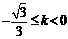 时,直线的倾斜角α满足
时,直线的倾斜角α满足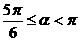
所以,直线的倾斜角的范围: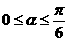 和
和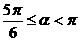
(2)利用直线方程的几何特征确定直线的位置
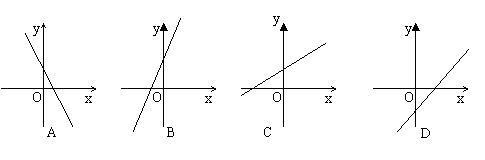 问题3:已知函数
问题3:已知函数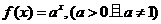 ,当
,当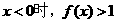 ,方程
,方程 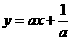 表示的直线是
表示的直线是
点拨:这是直线方程中的参数的几何意义问题,可先确定直线的斜率和截距的范围,再确定直线的位置,由已知可得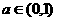 ,从而斜率
,从而斜率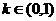 ,截距
,截距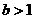 ,故选C
,故选C
(3)选择恰当的形式求直线方程
问题4:过点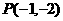 的直线分别交
的直线分别交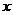 轴、
轴、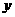 轴的负半轴于
轴的负半轴于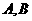 两点,当
两点,当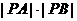 最小时,求直线
最小时,求直线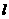 的方程。
的方程。
点拨:设直线方程要从条件和结论两方面考虑,为更好表示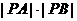 ,本题用点斜式设出方程最简便。
,本题用点斜式设出方程最简便。
解:设直线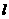 的方程为
的方程为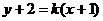 ,
,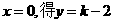 ,
,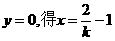 ,
,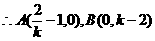 ,
,

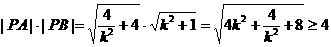 ,当且仅当
,当且仅当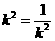 ,即k=±1时等号成立,但k<0,故直线
,即k=±1时等号成立,但k<0,故直线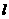 的方程为:x+y+3=0;
的方程为:x+y+3=0;
(4)设直线方程时要考虑是否会有丢解的情况,如:
问题5:求过点 ,且在
,且在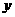 轴上的截距是在
轴上的截距是在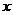 轴上的截距的2倍的直线方程。
轴上的截距的2倍的直线方程。
点拨: 设直线方程都要考虑是否丢解的问题,本题用截距式设直线方程容易漏掉过原点的直线,应警惕。
解:当直线过原点时,方程为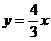 ;当直线不经过原点时,设方程为
;当直线不经过原点时,设方程为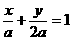 ,把
,把 代入得
代入得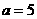 ,
, 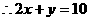
综上,所求方程为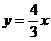 或
或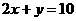
★热点考点题型探析★
考点1 直线的倾斜角和斜率
题型1 :已知倾斜角(或范围)求斜率(或范围)或已知斜率(或范围)求倾斜角(或范围)
[例1 ]已知经过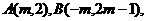 的直线的倾斜角为
的直线的倾斜角为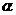 ,且
,且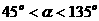 ,试求实数
,试求实数 的取值范围。
的取值范围。
[解题思路]由倾斜角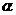 的范围得出斜率
的范围得出斜率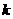 的范围,从而求出参数
的范围,从而求出参数 的取值范围.
的取值范围.
[解析]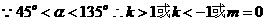 ,
,
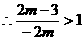 或
或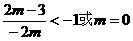 ,解得:
,解得: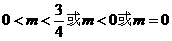
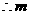 的取值范围是
的取值范围是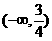
[名师指引]根据正切函数在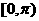 上的单调性,要分
上的单调性,要分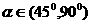 ;
;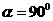
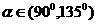 三种情况讨论,特别注意
三种情况讨论,特别注意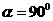 时容易遗漏.
时容易遗漏.
题型2 :动直线与线段(曲线段、区域)相交
 [例2 ]已知直线l:y=kx-2和两点P(1,2)、Q(-4,1),若l与线段PQ相交,求k的取值范围;
[例2 ]已知直线l:y=kx-2和两点P(1,2)、Q(-4,1),若l与线段PQ相交,求k的取值范围;
[解题思路]用运动的观点,结合图形得出倾斜角的范围,从而得出斜率取值范围
[解析]由直线方程y=kx-2可知直线过定点(0,-2),
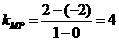
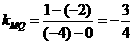
∵
∴要使直线l与线段PQ有交点,则k的取值范围
是k≥4和k≤-3/4
[名师指引](1)用“运动的观点”是解决这类问题的根本方法,注意“两条直线相交”和“直线与线段相交”的区别(2)在观察动直线在运动过程中,要特别注意倾斜角是否含有 角,若含有,则斜率的范围是
角,若含有,则斜率的范围是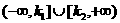 ,若不含有,则斜率的范围是
,若不含有,则斜率的范围是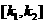 (
(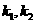 分别为线段端点与直线所过定点连线的斜率)
分别为线段端点与直线所过定点连线的斜率)
[新题导练]
2.直线方程的五种形式:
点斜式方程是 ;不能表示的直线为垂直于
;不能表示的直线为垂直于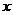 轴的直线
轴的直线
斜截式方程为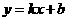 ;不能表示的直线为垂直于
;不能表示的直线为垂直于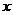 轴的直线
轴的直线
两点式方程为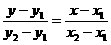 ;不能表示的直线为垂直于坐标轴的直线
;不能表示的直线为垂直于坐标轴的直线
截距式方程为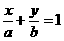 ;不能表示的直线为垂直于坐标轴的直线和过原点的直线.
;不能表示的直线为垂直于坐标轴的直线和过原点的直线.
一般式方程为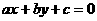 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com