
题目列表(包括答案和解析)
9.已知关于x的二次方程x2+2mx+2m+1=0.
(1)若方程有两根,其中一根在区间(-1,0)内,另一根在区间(1,2)内,求m的范围.
(2)若方程两根均在区间(0,1)内,求m的范围.
[解析](1)条件说明抛物线f(x)=x2+2mx+2m+1与x轴的交点分别在区间(-1,0)和(1,2)内,画出示意图,得


∴ .
.
(2)据抛物线与x轴交点落在区间(0,1)内,列不等式组


(这里0<-m<1是因为对称轴x=-m应在区间(0,1)内通过)
8.(2008·惠州调研)若函数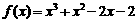 的一个正数零点附近的函数值用二分法计算,其参考数据如下:
的一个正数零点附近的函数值用二分法计算,其参考数据如下:



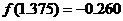


那么方程 的一个近似根(精确到0.1)为( ).
的一个近似根(精确到0.1)为( ).
A.1.2; B.1.3;C.1.4 ; D.1.5
7.(09年深圳宝安中学) 定义域和值域均为[-a,a] (常数a>0)的函数y=f(x)和y=g(x)的图像如图所示,给出下列四个命题中:
(1) 方程f[g(x)]=0有且仅有三个解; (2) 方程g[f(x)]=0有且仅有三个解;
(3) 方程f[f(x)]=0有且仅有九个解; (4)方程g[g(x)]=0有且仅有一个解。

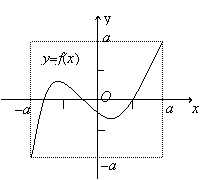 那么,其中正确命题的个数是( )
那么,其中正确命题的个数是( )
A. 1;B. 2;C. 3; D. 4
[解析] B;由图可知, ,
, ,由左图及f[g(x)]=0得
,由左图及f[g(x)]=0得
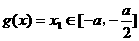 ,
, ,
, ,由右知方程f[g(x)]=0有且仅有三个解,即(1)正确;由右图及g[f(x)]=0得
,由右知方程f[g(x)]=0有且仅有三个解,即(1)正确;由右图及g[f(x)]=0得 ,由左图知方程g[f(x)]=0有且仅有一个解,故(2)错误;由左图及f[f(x)]=0得
,由左图知方程g[f(x)]=0有且仅有一个解,故(2)错误;由左图及f[f(x)]=0得 ,
, ,
, ,又由左图得到方程f[f(x)]=0最多有三个解,故(3)错误;由右图及g[g(x)]=0得
,又由左图得到方程f[f(x)]=0最多有三个解,故(3)错误;由右图及g[g(x)]=0得 ,由右图知方程g[g(x)]=0有且仅有一个解,即(4)正确,所以应选择B
,由右图知方程g[g(x)]=0有且仅有一个解,即(4)正确,所以应选择B
6.(09年韶关市第一次调研考)已知函数 ,若实数
,若实数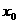 是方程
是方程 的解,且
的解,且 ,则
,则
的值( )
A.恒为正值;B.等于零;C. 恒为负值; D.不大于零
[解析] A.在同一坐标系中作出函数 和
和 的图象,发现
的图象,发现 ,并且当
,并且当 时,
时,
综合提高训练:
5.(金山中学09届月考)用二分法求方程 在区间
在区间 上的近似解,取区间中点
上的近似解,取区间中点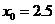 ,那么下一个有解区间为
,那么下一个有解区间为
[解析] 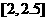 ;令
;令 ,则
,则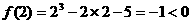
 ,故下一个有解区间为
,故下一个有解区间为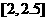
4.(湛江市09年高三统考)方程 的解所在区间是( )
的解所在区间是( )
A.(0,1) B.(1,2) C.(2,3) D.(3,4)
[解析] A;令 ,则
,则 ,
, ,所以方程
,所以方程 的解所在区间是(0,1)
的解所在区间是(0,1)
3.方程2x=2-x的解的个数为___________.
[解析]1;方程2x=2-x的解可看作函数y=2x和y=2-x的图象交点的横坐标,分别作出这两个函数图象(如下图).

由图象得只有一个交点,因此该方程只有一个解.
2.(华侨中学09届月考)设函数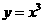 与
与 的图象的交点为
的图象的交点为 ,则
,则 所在的区间是( )
所在的区间是( )
A. ;B.
;B. ;C.
;C. ;D.
;D.
[解析] B;令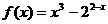 ,则
,则 ,
,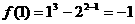 ,
, ,可见
,可见 所在的区间是
所在的区间是
1. (深圳九校09届联考)下图是函数
(深圳九校09届联考)下图是函数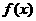 的图像,
的图像,
它与 轴有
轴有 个不同的公共点.给出下列四个区间,
个不同的公共点.给出下列四个区间,
不能用二分法求出函数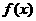 在区间( )上的零点
在区间( )上的零点
A. ;B.
;B.
C. ;D.
;D.
[解析] B;由于用二分法判断函数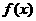 在区间
在区间 上有零点的必要条件是
上有零点的必要条件是
 ,而从图可以看出,
,而从图可以看出,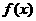 在区间
在区间 的两端的符号相同,故不能
的两端的符号相同,故不能
用二分法求出函数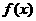 在这个区间上的零点
在这个区间上的零点
5.(2007·韶关)若关于x的方程4x+2x a+a+1=0有实数根,求实数a的取值范围.
[解析]令t=2x, t>0
t>0 关于x的方程4x+2x a+a+1=0有实数根等价于方程t2+at+a+1=0(t>0)有正实数根,令f(t)=
t2+at+a+1,且
关于x的方程4x+2x a+a+1=0有实数根等价于方程t2+at+a+1=0(t>0)有正实数根,令f(t)=
t2+at+a+1,且 故方程t2+at+a+1=0(t>0)有正实数根等价于(1)方程有一个正根一个负根:由f(0)<0,得a<-1
故方程t2+at+a+1=0(t>0)有正实数根等价于(1)方程有一个正根一个负根:由f(0)<0,得a<-1
(2)方程有两个相等的正数根:由
(3)方程有两个不相等的正数根或有一个零根一个正根时:
由
求(1)(2)(3)的并集,得实数a的取值范围: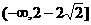
 [备选例题] (佛山市三水中学09届)下图是函数
[备选例题] (佛山市三水中学09届)下图是函数
 和
和 图象的一部分,其中
图象的一部分,其中
 时,两函数值相等.
时,两函数值相等.
(1)给出如下两个命题:①当 时,
时, ;
;
②当 时,
时, .判断命题①②的真假并说明理由.
.判断命题①②的真假并说明理由.
(2)求证:
[解析](1) 命题①是假命题,反例: ,则
,则 ,但是
,但是
 ,
, 不成立.
不成立.
命题②是真命题,因为 在
在 上是减函数,函数
上是减函数,函数 在
在 上是增函数,所以当
上是增函数,所以当 时,
时, .
.
(2)构造函数 ,则
,则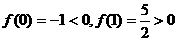 ,所一
,所一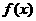 在区间
在区间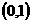 有零点.有因为
有零点.有因为 在区间
在区间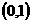 是增函数,所以
是增函数,所以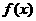 在区间
在区间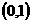 有唯一个零点,即
有唯一个零点,即 ,所以
,所以 .
.
★抢分频道
基础巩固训练:
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com