
题目列表(包括答案和解析)
2. 点 在
在 平面上的投影点
平面上的投影点 的坐标是
(
)
的坐标是
(
)
A. B.
B. C.
C.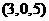 D.
D. 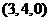
解析:两点的纵坐标、竖坐标不变,选B
1.将空间直角坐标系(右手系)画在纸上时,我们通常将 轴与
轴与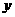 轴,
轴, 轴与
轴与 轴所成的角画成( )
轴所成的角画成( )
A.
 B.
B. C.
C. D.
D.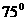
解析:选B
6.已知三点 ,是否存在实数
,是否存在实数 ,使A、B、C共线?若存在,求出
,使A、B、C共线?若存在,求出 的值;若不存在,说明理由。
的值;若不存在,说明理由。
[解析]  ,
,
 ,
,
 ,
,
因为 ,所以,若
,所以,若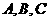 三点共线,有
三点共线,有 或
或 ,
,
若 ,整理得:
,整理得: ,此方程无解;
,此方程无解;
若 ,整理得:
,整理得: ,此方程也无解。
,此方程也无解。
所以不存在实数 ,使A、B、C共线。
,使A、B、C共线。
★抢分频道★
基础巩固训练
5.已知球面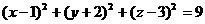 ,与点
,与点 ,则球面上的点与点
,则球面上的点与点 距离的最大值与最小值分别是
。
距离的最大值与最小值分别是
。
[解析]球心 ,球面上的点与点
,球面上的点与点 距离的最大值与最小值分别是9和3
距离的最大值与最小值分别是9和3
4.已知 ,当
,当 两点间距离取得最小值时,
两点间距离取得最小值时, 的值为 ( )
的值为 ( )
A.19
B.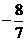 C.
C.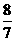 D.
D.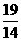
[解析]
当
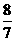 时,
时, 取得最小值
取得最小值
3.已知 ,记
,记 到
到 轴的距离为
轴的距离为 ,
, 到
到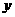 轴的距离为
轴的距离为 ,
, 到
到 轴的距离为
轴的距离为 ,则( )
,则( )
A. B.
B. C.
C.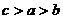 D.
D.
[解析]借助长方体来思考,  、
、 、
、 分别是三条面对角线的长度。
分别是三条面对角线的长度。 ,选C
,选C
考点2:空间两点间的距离公式
题型:利用空间两点间的距离公式解决有关问题
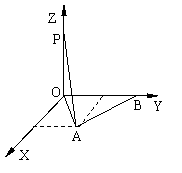 [例3 ] 如图:已知点
[例3 ] 如图:已知点 ,对于
,对于 轴正半轴上任意一点
轴正半轴上任意一点 ,在
,在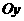 轴上是否存在一点
轴上是否存在一点 ,使得
,使得 恒成立?若存在,求出
恒成立?若存在,求出 点的坐标;若不存在,说明理由。
点的坐标;若不存在,说明理由。
[解题思路]转化为距离问题,即证明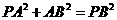
[解析]设 
 ,
,
对于 轴正半轴上任意一点
轴正半轴上任意一点 ,假设在
,假设在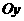 轴上存在一点
轴上存在一点 ,使得
,使得 恒成立,
恒成立,
则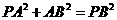
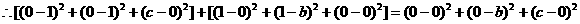 即
即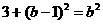 ,解得:
,解得: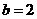
所以存在这样的点 ,当点
,当点 为
为 时,
时, 恒成立
恒成立
[名师指引]在空间直角坐标系中,利用距离可以证明垂直问题。此外,用距离还可以解决空间三点共线问题和求简单的点的轨迹。
[新题导练]
2.平行四边形 的两个顶点的的坐标为
的两个顶点的的坐标为 ,对角线的交点为
,对角线的交点为 ,则顶点C的坐标为 , 顶点D的坐标为
,则顶点C的坐标为 , 顶点D的坐标为
[解析]由已知得线段 的中点为
的中点为 ,线段
,线段 的中点也是
的中点也是 ,由中点坐标公式易得
,由中点坐标公式易得
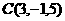 ,
,
1.已知正四棱柱 的顶点坐标分别为
的顶点坐标分别为 ,
, ,则
,则 的坐标为
。
的坐标为
。
[解析]正四棱柱 过点A的三条棱恰好是坐标轴,
过点A的三条棱恰好是坐标轴,

 的坐标为(2,2,5)
的坐标为(2,2,5)
3.利用空间两点间的距离公式,可以解决的几类问题
(1)判断两条相交直线是否垂直
(2)判断空间三点是否共线
(3)得到一些简单的空间轨迹方程
★热点考点题型探析★
考点1: 空间直角坐标系
题型1: 认识空间直角坐标系
[例1 ](1)在空间直角坐标系中, 表示
( )
表示
( )
A.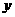 轴上的点
B.过
轴上的点
B.过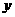 轴的平面
轴的平面
C.垂直于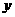 轴的平面
D.平行于
轴的平面
D.平行于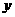 轴的直线
轴的直线
(2)在空间直角坐标系中,方程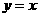 表示
表示
A.在坐标平面 中,1,3象限的平分线 B.平行于
中,1,3象限的平分线 B.平行于 轴的一条直线
轴的一条直线
C.经过 轴的一个平面
D.平行于
轴的一个平面
D.平行于 轴的一个平面
轴的一个平面
[解题思路]认识空间直角坐标系,可以类比平面直角坐标系,如在平面直角坐标系坐标系中, 方程 表示所有横坐标为1的点的集合
表示所有横坐标为1的点的集合
[解析](1) 表示所有在
表示所有在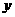 轴上的投影是点
轴上的投影是点 的点的集合,所以
的点的集合,所以 表示经过点
表示经过点 且垂直于
且垂直于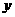 轴的平面
轴的平面
(2)方程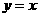 表示在任何一个垂直于
表示在任何一个垂直于 轴的一个平面内,1,3象限的平分线组成的集合
轴的一个平面内,1,3象限的平分线组成的集合
[名师指引](1)类比平面直角坐标系,可以帮助我们认识空间直角坐标系
(2)要从满足某些特殊条件的点的坐标特征去思考问题。如:
经过点 且垂直于
且垂直于 轴的平面上的点都可表示为
轴的平面上的点都可表示为
题型2: 空间中点坐标公式与点的对称问题
[例2 ] 点 关于
关于 轴的对称点为
轴的对称点为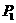 ,点
,点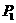 关于平面
关于平面 的对称点为
的对称点为 ,则
,则 的坐标为
的坐标为
[解题思路]类比平面直角坐标系中的对称关系,得到空间直角坐标系中的对称关系
[解析]因点 和
和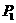 关于
关于 轴对称, 所以点
轴对称, 所以点 和
和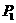 的竖坐标相同,且在平面
的竖坐标相同,且在平面 的射影关于原点对称,故点
的射影关于原点对称,故点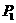 的坐标为
的坐标为 ,
,
又因点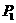 和
和 关于平面
关于平面 对称, 所以点
对称, 所以点 坐标为
坐标为
[名师指引]解决空间点的对称问题,一要借助空间想象,二要从它们在坐标平面的射影找关系,如借助空间想象,在例2中可以直接得出点 为点
为点 关于原点的对称点,故坐标为
关于原点的对称点,故坐标为
[新题导练]
2.将平面直角坐标系类比到空间直角坐标系
问题2:对于任意实数 ,求
,求 的最小值
的最小值
[解析]在空间直角坐标系中, 表示空间点
表示空间点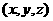 到点
到点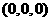 的距离与到点
的距离与到点 的距离之和,它的最小值就是点
的距离之和,它的最小值就是点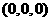 与点
与点 之间的线段长,所以
之间的线段长,所以 的最小值为
的最小值为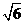 。
。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com