
题目列表(包括答案和解析)
3.指数型的方程和不等式的解法
(Ⅰ)形如 的形式常用“化同底”转化为利用指数函数的单调性解决,或“取对数”等方法;
的形式常用“化同底”转化为利用指数函数的单调性解决,或“取对数”等方法;
(Ⅱ)形如 或
或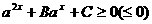 的形式,可借助于换元法转化为二次方程或不等式求解。
的形式,可借助于换元法转化为二次方程或不等式求解。
★热点考点题型探析
考点1 指数幂的运算
[例1] (湛江市09届统考)计算:
[解题思路] 根式的形式通常写成分数指数幂后进行运算。
[解析]原式
[名师指引]根式的运算是基本运算,在未来的高考中一般不会单独命题,而是与其它知识结合在一起,比如与二项展开式结合就比较常见
[新题导练]
①指数函数的定义:一般地,函数y=ax(a>0且a≠1)叫做指数函数.
②指数函数的图像

③底数互为倒数的两个指数函数的图像关于y轴对称.
④指数函数的性质:定义域:R; 值域:(0,+∞);过点(0,1);即x=0时,y=1.
当a>1时,在R上是增函数;当0<a<1时,在R上是减函数.
画指数函数y=ax(a>0且a≠1)的图像时,应该抓住两点:一是过定点(0,1),二是x轴
是其渐近线
★重、难点突破
重点:有理指数幂的定义及性质,指数函数的概念、图像与性质
难点:综合运用指数函数的图像与性质解决问题
重难点:1.指数型函数单调性的判断,方法主要有两种:
(1)利用单调性的定义(可以作差,也可以作商)
 (2)利用复合函数的单调性判断形如
(2)利用复合函数的单调性判断形如 的函数的单调性:若
的函数的单调性:若 ,则
,则 的单调增(减)区间,就是
的单调增(减)区间,就是 的单调增(减)区间;若
的单调增(减)区间;若 ,则
,则 的单调增(减)区间,就是
的单调增(减)区间,就是 的单调减(增)区间;
的单调减(增)区间;
2. 指数函数的图像与性质
(Ⅰ) 指数函数在同一直角坐标系中的图象的相对位置与底数大小的关系如图所示,对
应关系为
(1)y=ax,(2)y=bx,(3)y=cx,(4)y=dx
则
在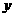 轴右侧,图象从上到下相应的底数由大变小;在
轴右侧,图象从上到下相应的底数由大变小;在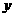 轴左侧,图象从下到上相应的底数由大变小,即无论在
轴左侧,图象从下到上相应的底数由大变小,即无论在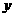 轴左侧还是右侧,底数按逆时针方向变大.
轴左侧还是右侧,底数按逆时针方向变大.
(Ⅱ) 指数函数的图像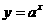 与
与 的图象关于
的图象关于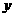 轴对称
轴对称
10. 如图,以棱长为
如图,以棱长为 的正方体的三条棱为坐标轴,建立空间直角坐标系
的正方体的三条棱为坐标轴,建立空间直角坐标系 ,点
,点 在正方体的对角线
在正方体的对角线 上,点
上,点 在正方体的棱
在正方体的棱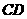 上。
上。
(1)当点 为对角线
为对角线 的中点,点
的中点,点 在棱
在棱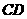 上运动时,
上运动时,
探究 的最小值;
的最小值;
(2)当点 在对角线
在对角线 上运动,点
上运动,点 为棱
为棱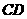 的中点时,
的中点时,
探究 的最小值;
的最小值;
[解析]由已知 ,
,
(1)当点 为对角线
为对角线 的中点时,点
的中点时,点 坐标为
坐标为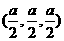 ,
,
设 ,则
,则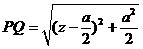 ,
,
当 时,
时, 取到最小值为
取到最小值为 ,此时
,此时 为
为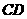 的中点。
的中点。
(2)当点 为棱
为棱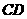 的中点时,点
的中点时,点 的坐标为
的坐标为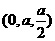 ,设
,设 ,则
,则 ,
,
 ,
, ,所以
,所以 点的坐标为
点的坐标为 ,
,
所以 ,当
,当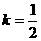 ,即
,即 为
为 的中点时,
的中点时, 取到最小值
取到最小值 。
。
9.(2008年佛冈一中模拟)已知空间直角坐标系 中有一点
中有一点 ,点
,点 是平面
是平面 内的直线
内的直线 上的动点,则
上的动点,则 两点的最短距离是( )
两点的最短距离是( )
A. B.
B. C.3
D.
C.3
D. 
[解析]因为点B在 平面内的直线
平面内的直线 上,故可设点B为
上,故可设点B为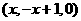 ,
,
所以 ,
,
所以当 时,AB取得最小值
时,AB取得最小值 ,此时点B为
,此时点B为 。
。
8.(2007山东昌乐模拟)三角形 的三个顶点的坐标为
的三个顶点的坐标为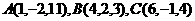 ,则
,则 的形状为( )
的形状为( )
A.正三角形 B.锐角三角形 C.直角三角形 D.钝角三角形
[解析] C


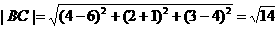

7.空间直角坐标系中,到坐标平面 ,
, ,
, 的距离分别为2,2,3的点有
的距离分别为2,2,3的点有
A.1个 B.2个 C.4个 D.8个
解析:8个。分别为(3,2,2)、(3,2,-2)、(3,-2,2)、(3,-2,-2)、(-3,2,2)、(-3,2,-2)、(-3,-2,2)、(-3,-2,-2)
6.正方体不在同一表面上的两顶点P(-1,2,-1),Q(3,-2,3),则正方体的体积是
[解析] 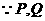 不共面,
不共面, 为正方体的一条对角线,
为正方体的一条对角线, ,正方体的棱长为4,体积为64
,正方体的棱长为4,体积为64
综合提高训练
5.(2007年湛江模拟)点 关于
关于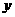 轴的对称点为
轴的对称点为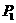 ,
,  关于平面
关于平面 的对称点为
的对称点为 ,则
,则 =
=
[解析] 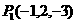 ,
,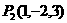 ,
,
4.(2007山东济宁模拟)设点B是点A(2,-3,5)关于平面 的对称点,则|AB|等于(
)
的对称点,则|AB|等于(
)
A.10
B. C.
C. D.38
D.38
[解析] A
点A(2,-3,5)关于平面 的对称点为
的对称点为 ,
,

3. 三棱锥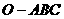 中,
中,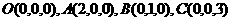 此三棱锥的体积为( )
此三棱锥的体积为( )
A.1 B.2 C.3 D. 6
[解析]  两两垂直,
两两垂直,
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com