
题目列表(包括答案和解析)
1.(高州中学09届月考)与函数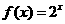 的图像关于直线
的图像关于直线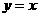 对称的曲线C对应的函数为
对称的曲线C对应的函数为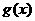 ,则
,则 的值为 ( )
的值为 ( )
A. ;B.
;B. ;C.
;C. ;D.
;D.
[解析] D;依题意得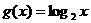 ,所以
,所以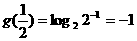
9.设 ,如果当
,如果当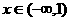 时
时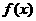 有意
有意
义,求a的取值范围.
[解析] 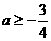 ;当
;当 时,
时,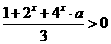 恒成立,即
恒成立,即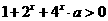 恒成立
恒成立
∴
令 ,则
,则 时,
时, ,∴
,∴
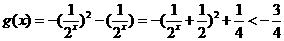 ,∴
,∴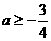
[备选例题] (广州六校09届联考)已知函数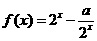 , 将
, 将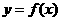 的图象向右平移两个单位, 得到
的图象向右平移两个单位, 得到 的图象.
的图象.
(1) 求函数 的解析式;
的解析式;
(2) 若函数 与函数
与函数 的图象关于直线
的图象关于直线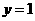 对称, 求函数
对称, 求函数 的解析式;
的解析式;
[解析] (1) 由题设得 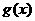
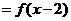
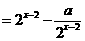
(2) 设点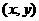 在
在 的图象上, 点
的图象上, 点 在
在 的图象上, 且与点
的图象上, 且与点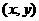 关于直线
关于直线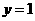 对称, 则
对称, 则
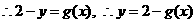
即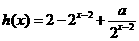 .
.
★抢分频道
基础巩固训练:
8.(2008上海) 已知函数 ,若
,若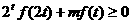 对于
对于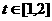 恒成立,求实数
恒成立,求实数 的取值范围
的取值范围
[解析] 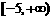 ;当
;当
即 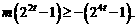


故m的取值范围是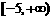
7.(08年安徽改编)若函数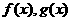 分别是
分别是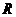 上的奇函数、偶函数,且满足
上的奇函数、偶函数,且满足 ,则
,则 、
、 、
、 的大小关系为
的大小关系为
[解析]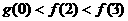 ;因为
;因为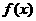 是奇函数,
是奇函数,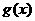 是偶函数,所以有
是偶函数,所以有
 ,得
,得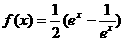 ,可见
,可见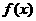 在
在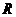 上是增函数,故
上是增函数,故 ,又由
,又由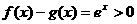 知
知 ,因此
,因此
所以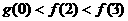
考点3 与指数函数有关的含参数问题
[例5] 要使函数y=1+2x+4xa在x∈(-∞,1]上y>0恒成立,求a的取值范围.
[解题思路]欲求 的取值范围,应该由1+2x+4x
的取值范围,应该由1+2x+4x >0将参数
>0将参数 分离,转变为求函数的最值
分离,转变为求函数的最值
[解析] 由题意,得1+2x+4xa>0在x∈(-∞,1]上恒成立,即a>-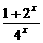 在
在
x∈(-∞,1]上恒成立.又∵-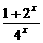 =-(
=-(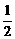 )2x-(
)2x-(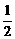 )x=-[(
)x=-[(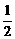 )x+
)x+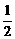 ]2+
]2+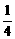 ,
,
当x∈(-∞,1]时值域为(-∞,-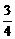 ],∴a>-
],∴a>-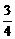
[名师指引]①由某个不等式在某个范围内恒成立,求参数的取值范围是高考中的热点,处理的方法往往是通过分离参数, 转变为求函数的最值,但要注意端点的值能否取到;
②指数函数的综合问题常常涉及指数函数的定义域、值域、过定点、单调性、奇偶性、图像特征,要用到数形结合思想、分类讨论思想.
③指数函数是重要的基本初等函数, 高考中既考查双基, 又考查对蕴含其中的函数思想、等价转化、分类讨论等思想方法的理解与运用. 因此应做到能熟练掌握它们的图像与性质并能进行一定的综合运用。
[新题导练]
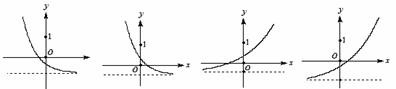
6.(广东广雅中学09届月考)已知函数 (其中
(其中 )的图象如下面右图所示,则函数
)的图象如下面右图所示,则函数 的图象是( )
的图象是( )

A. B. C. D.
[解析] A;由 的图象知
的图象知 ,所以函数
,所以函数 的图象是A
的图象是A
5.(广东恩城中学09年模拟)不论 为何正实数,函数
为何正实数,函数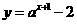 的图象一定通过一定点,则该定点的坐标是_________
的图象一定通过一定点,则该定点的坐标是_________
[解析] ;因为函数
;因为函数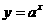 的图象通过定点
的图象通过定点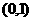 ,故函数
,故函数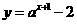 的图象一定通过定点
的图象一定通过定点
4.(金山中学09届月考)若直线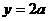 与函数
与函数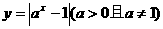 的图象有两个公共点,则a的取值范围是_______.
的图象有两个公共点,则a的取值范围是_______.
[解析]  ;画出函数
;画出函数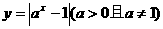 的草图知,若直线
的草图知,若直线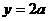 与函数
与函数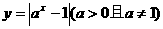 的图象有两个公共点,则
的图象有两个公共点,则 ,即
,即
3.不等式 的解集是___________
的解集是___________
[解析]  ;由不等式
;由不等式 得
得 ,解得
,解得
2. 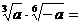
[解析]  ;
; 
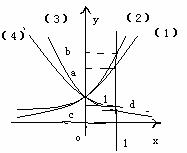 考点2 指数函数的图象及性质的应用
考点2 指数函数的图象及性质的应用
题型1:由指数函数的图象判断底数的大小
[例2] 下图是指数函数(1)y=ax,(2)y=bx,(3)y=cx,(4)y=dx的图像,则a、b、c、d与1的大小关系是( )
A.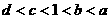 ; B.
; B. ;
;
C. ;D.
;D.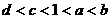
[解题思路] 显然,作为直线x=1即可发现a、b、c、d与1的大小关系
[解析] B;令x=1,由图知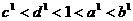 ,即
,即
[名师指引] 由指数函数的图象确定底数的大小关系,关键要从具体图象进行分析
题型2:解简单的指数方程
[例3] 方程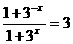 的解是_________
的解是_________
[解题思路]将方程化为最简单的指数方程
[解析] ;在方程
;在方程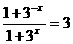 的两边同时乘以
的两边同时乘以 得
得 ,从而得
,从而得
所以
[名师指引]解指数方程要观察其特征,在本题中,关键是发现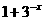 与
与 的关系:
的关系:
题型3:利用函数的单调性求函数的值域
[例4] 已知2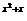 ≤(
≤(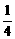 )x-2,求函数y=2x-2-x的值域.
)x-2,求函数y=2x-2-x的值域.
[解题思路]求函数y=2x-2-x的值域应利用考虑其单调性
[解析] ∵2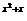 ≤2-2(x-2),∴x2+x≤4-2x,即x2+3x-4≤0,得-4≤x≤1.
≤2-2(x-2),∴x2+x≤4-2x,即x2+3x-4≤0,得-4≤x≤1.
又∵y=2x-2-x是[-4,1]上的增函数,∴2-4-24≤y≤2-2-1.
故所求函数y的值域是[- ,
,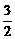 ].
].
[名师指引]利用函数的单调性确定其值域是高考热点,关键在于发现函数的单调性
[新题导练]
1.(高州中学09届月考)经化简后,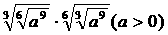 的结果是
的结果是
[解析]  ;
;
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com