1．由四舍五入得到的近似数0.600的有效数字是________．

7．用四舍五入法得到的近似数 ，其准确数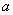 的范围是() ．

　A． B ．

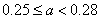　C． D．

6．近似数5和 的准确值的取值范围大小关系是() ．

　A． 的取值范围大　B．5的取值范围大

　C．取值范围相同　　D．不能确定

5．若有两个数 、 ，用四舍五入法得到的近似数分别是 和 ，则 、 应满足() ．

　A． 的精确度高B． 的精确度高

　C． 与 的精确度相同D． ， 的精确度不能确定

4．下列说法正确的是() ．

　A．近似数4000和4万的精确度一样

　B．将圆周率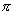 精确到千分位后有四个有效数字3、1、4、2

　C．近似数 与近似数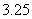 的精确度一样

　D．354600精确到万位是350000

3．将数375800精确到万位的近似数是() ．

　A．38B．380000C．37. 6万D．

2．将近似数 精确到 时，有效数字有() ．

　A．5、1、9B．5、2C．5、2、0D．5、l、9、7

1．由四舍五入得到的近似数 ，它的精确度是精确到() ．

　A．十分位B．百分位C．千分位D．万分位

　(2)某歌星在体育馆举办音乐会，大约有一万二千人参加；

　(3)通过计算，直径为10cm的圆的周长是31.4cm；

　(4)检查一双没洗过的手，发现带有各种细菌80000万个；

　(5)1999年我国国民经济增长7.8%．

　解：(1)43是准确数．因为43是质数，求平均数时不一定除得尽，所以82.5一般是近似数；

　(2)一万二千是近似数；

　(3)10是准确数，因为3.14是π的近似值，所以31.4是近似数；

　(4)80000万是近似数；

　(5)1999是准确数，7.8%是近似数．

　说明：1．在近似数的计算中，分清准确数和近似数是很重要的，它是决定我们用近似计算法则进行计算，还是用一般方法进行计算的依据．

2．产生近似数的主要原因：

　(1)“计算”产生近似数．如除不尽，有圆周率π参加计算的结果等等；

　(2)用测量工具测出的量一般都是近似数，如长度、重量、时间等等；

　(3)不容易得到，或不可能得到准确数时，只能得到近似数，如人口普查的结果，就只能是一个近似数；

　(4)由于不必要知道准确数而产生近似数．

　例2　下列由四舍五入得到的近似数，各精确到哪一位？各有哪几个有效数字？

　(1)38200 　　(2)0.040　 　(3)20.05000 　　(4)4×10⁴

　分析：对于一个四舍五入得到的近似数，如果是整数，如38200，就精确到个位；如果有一位小数，就精确到十分位；两位小数，就精确到百分位；象0.040有三位小数就精确到千分位；象20.05000就精确到十万分位；而4×10⁴=40000，只有一个有效数字4，则精确到万位．有效数字的个数应按照定义计算．

　解：(1)38200精确到个位，有五个有效数字3、8、2、0、0．

　(2)0.040精确到千分位(即精确到0.001)有两个有效数字4、0．

　(3)20.05000精确到十万分位(即精确到0.00001)，

　有七个有效数字2、0、0、5、0、0、0．

　(4)4×10⁴精确到万位，有一个有效数字4．

　说明：(1)一个近似数的位数与精确度有关，不能随意添上或去掉末位的零．如20.05000的有效数字是2、0、0、5、0、0、0七个．而20.05的有效数字是2、0、0、5四个．因为20.05000精确到0.00001，而20.05精确到0.01，精确度不一样，有效数字也不同，所以右边的三个0不能随意去掉．

　(2)对有效数字，如0.040，4左边的两个0不是有效数字，4右边的0是有效数字．

　(3)近似数40000与4×10⁴有区别，40000表示精确到个位，有五个有效数字4、0、0、0、0，而4×10⁴表示精确到万位，有1个有效数字4．

　例3 下列由四舍五入得到的近似数，各精确到哪一位？各有几个有效数字？

　(1)70万；(2)9.03万；　(3)1.8亿；　(4)6.40×10⁵

　分析：因为这四个数都是近似数，所以：(1)的有效数字是2个：7、0，0不是个位，而是“万”位；(2)的有效数字是3个：9、0、3，3不是百分位，而是“百”位；(3)的有效数字是2个：1、8，8不是十分位，而是“千万”位；(4)的有效数字是3个：6、4、0，0不是百分位，而是“千”位．

　解：(1)70万. 精确到万位，有2个有效数字7、0；

　(2)9.03万.精确到百位，有3个有效数字9、0、3；

　(3)1.8亿.精确到千万位，有2个有效数字1、8；

　(4)6.40×10⁵.精确到千位，有3个有效数字6、4、0．

　说明：较大的数取近似值时，常用×万，×亿等等来表示，这里的“×”表示这个近似数的有效数字，而它精确到的位数不一定是“万”或“亿”．对于不熟练的学生，应当写出原数之后再判断精确到哪一位，例如9.03万=90300，因为“3”在百位上，所以9.03万精确到百位．

　例4　用四舍五入法，按括号里的要求对下列各数取近似值．

　(1)1.5982(精确到0.01)　(2)0.03049(保留两个有效数字)

　(3)3.3074(精确到个位)　(4)81.661(保留三个有效数字)

　分析：四舍五入是指要精确到的那一位后面紧跟的一位，如果比5小则舍，如果比5大或等于5则进1，与再后面各位数字的大小无关．

　(1)1.5982要精确到0.01即百分位，只看它后面的一位即千分位的数字，是8＞5，应当进1，所以近似值为1.60．

　(2)0.03049保留两个有效数字，3左边的0不算，从3开始，两个有效数字是3、0，再看第三个数字是4＜5，应当舍，所以近似值为0.030．

　(3)、(4)同上．

　解：(1)1.5982≈1.60　(2)0.03049≈0.030

　(3)3.3074≈3　(4)81.661≈81.7

　说明：1.60与0.030的最后一个0都不能随便去掉．1.60是表示精确到0.01，而1.6表示精确到0.1．对0.030，最后一个0也是表示精确度的，表示精确到千分位，而0.03只精确到百分位．

　例5　用四舍五入法，按括号里的要求对下列各数取近似值，并说出它的精确度(或有效数字)．

　(1)26074(精确到千位)　(2)7049(保留2个有效数字)

　(3)26074000000(精确到亿位)　(4)704.9(保留3个有效数字)

　分析：根据题目的要求：(1)26074≈26000；(2)7049≈7000；(3)26074000000≈26100000000；(4)704.9≈705；(1)、(2)、(3)题的近似值中看不出它们的精确度，所以必须用科学记数法表示．

　解：(1)26074=2.6074×10⁴≈2.6×10⁴，精确到千位，有2个有效数字2、6．

　(2)7049=7.049×10³≈7.0×10³，精确到百位，有两个有效数字7、0．

　(3)26074000000=2.6074×10¹⁰≈2.61×10¹⁰，

　精确到亿位，有三个有效数字2、6、1．

　(4)704.9≈705，精确到个位，有三个有效数字7、0、5．

　说明：求整数的近似数时，应注意以下两点：(1)近似数的位数一般都与已知数的位数相同；(2)当近似数不是精确到个位，或有效数字的个数小于整数的位数时，一般用科学记数法表示这个近似数．因为形如a×10n(1≤a＜10，n为正整数＝的数可以体现出整数的精确度．

习题精选

5．用计算器计算下列各式，将结果填写在横线上．

　 _______； _______；

　 _______； _______．

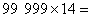　(1)你发现了什么？

　(2)不用计算器，你能直接写出 吗？