2、如图2，已知∠B＝∠C，则∠ADC与∠AEB的大小关系是：

A、∠ADC＞∠AEB　　　B、∠ADC＜∠AEB

C、∠ADC＝∠AEB　　　D、大小关系不能确定

1、以下列各组长度的线段为边，能构成三角形的是：

A．7cm，5cm，12cm　　　　 B．6cm，8cm，15cm

C．4cm，6cm，5cm　　　　D．8cm，4cm，3cm

2．某小组20名同学的数学测验成绩如下，试计算他们的平均分．

　81，72，77，83，73，85，92，84，75，63，76，97，80，90，76，91，86，78，74，85．

1．计算下列各式的值：

　(1)-1+3-5+7-9+11-…-1997+1999；

　(2)11+12-13-14+15+16-17-18+…+99+100；

　(3)1991×1999-1990×2000；

　(4)472634²+472 635²-472 633×472 635-472 634×472 636；

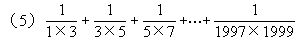
　(6)1+4+7+…+244；

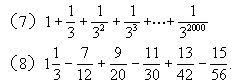
3．观察算式找规律

　例11 某班20名学生的数学期末考试成绩如下，请计算他们的总分与平均分．

　87，91，94，88，93，91，89，87，92，86，90，92，88，90，91，86，89，92，95，88．

　分析与解 若直接把20个数加起来，显然运算量较大，粗略地估计一下，这些数均在90上下，所以可取90为基准数，大于90的数取“正”，小于90的数取“负”，考察这20个数与90的差，这样会大大简化运算．所以总分为

　90×20+(-3)+1+4+(-2)+3+1+(-1)+(-3)

　　+2+(-4)+0+2+(-2)+0+1+(-4)+(-1)

　　+2+5+(-2)

　=1800-1=1799，

　平均分为 90+(-1)÷20=89.95．

　例12 计算1+3+5+7+…+1997+1999的值．

　分析 观察发现：首先算式中，从第二项开始，后项减前项的差都等于2；其次算式中首末两项之和与距首末两项等距离的两项之和都等于2000，于是可有如下解法．

　解 用字母S表示所求算式，即

S=1+3+5+…+1997+1999． ①

　再将S各项倒过来写为

S=1999+1997+1995+…+3+1． ②

　将①，②两式左右分别相加，得

　2S=(1+1999)+(3+1997)+…+(1997+3)+(1999+1)

　　=2000+2000+…+2000+2000(500个2000)

　　=2000×500．

　从而有 S=500 000．

　说明 一般地，一列数，如果从第二项开始，后项减前项的差都相等(本题3-1=5-3=7-5=…=1999-1997，都等于2)，那么，这列数的求和问题，都可以用上例中的“倒写相加”的方法解决．

　例13 计算 1+5+5²+5³+…+5⁹⁹+5¹⁰⁰的值．

　分析 观察发现，上式从第二项起，每一项都是它前面一项的5倍．如果将和式各项都乘以5，所得新和式中除个别项外，其余与原和式中的项相同，于是两式相减将使差易于计算．

　解 设

S=1+5+52+…+5⁹⁹+5¹⁰⁰， ①

　所以

5S=5+5²+5³+…+5¹⁰⁰+5¹⁰¹． ②

　②-①得

4S=5¹⁰¹-1，

　说明 如果一列数，从第二项起每一项与前一项之比都相等(本例中是都等于5)，那么这列数的求和问题，均可用上述“错位相减”法来解决．

　例14 计算：

　分析 一般情况下，分数计算是先通分．本题通分计算将很繁，所以我们不但不通分，反而利用如下一个关系式

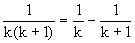
来把每一项拆成两项之差，然后再计算，这种方法叫做拆项法．

　解 由于

　所以

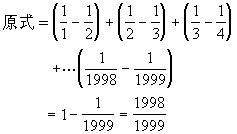
　说明 本例使用拆项法的目的是使总和中出现一些可以相消的相反数的项，这种方法在有理数巧算中很常用．

练习一

2．用字母表示数

　我们先来计算(100+2)×(100-2)的值：

(100+2)×(100-2)=100×100-2×100+2×100-4

=100²-2²．

　这是一个对具体数的运算，若用字母a代换100，用字母b代换2，上述运算过程变为

(a+b)(a-b)=a²-ab+ab-b²=a²-b²．

　于是我们得到了一个重要的计算公式

(a+b)(a-b)=a²-b²， ①

　这个公式叫平方差公式，以后应用这个公式计算时，不必重复公式的证明过程，可直接利用该公式计算．

　例5 计算 3001×2999的值．

　解 3001×2999=(3000+1)(3000-1)

=3000²-1²=8 999 999．

　例6 计算 103×97×10 009的值．

　解 原式=(100+3)(100-3)(10000+9)

=(100²-9)(100²+9)

=100⁴-9²=99 999 919．

　例7 计算：

　分析与解 直接计算繁．仔细观察，发现分母中涉及到三个连续整数：12 345，12 346，12 347．可设字母n=12 346，那么12 345=n-1，12 347=n+1，于是分母变为n²-(n-1)(n+1)．应用平方差公式化简得

n²-(n²-1²)=n²-n²+1=1，

　即原式分母的值是1，所以原式=24 690．

　例8 计算：

(2+1)(2²+1)(2⁴+1)(2⁸+1)(2¹⁶+1)(2³²+1)．

　分析 式子中2，2²，2⁴，…每一个数都是前一个数的平方，若在(2+1)前面有一个(2-1)，就可以连续递进地运用(a+b)(a-b)=a²-b²了．

　解 原式=(2-1)(2+1)(2²+1)(2⁴+1)(2⁸+1)×(2¹⁶+1)(2³²+1)

　 　　=(2²-1)(2²+1)(2⁴+1)(2⁸+1)(2¹⁶+1)×(2³²+1)

　　　 =(2⁴-1)(2⁴+1)(2⁸+1)(2¹⁶+1)(2³²+1)=……

　　 　=(2³²-1)(2³²+1)

　　　 =2⁶⁴-1．

　例9 计算：

　分析 在前面的例题中，应用过公式

(a+b)(a-b)=a²-b²．

　这个公式也可以反着使用，即

a²-b²=(a+b)(a-b)．

　本题就是一个例子．

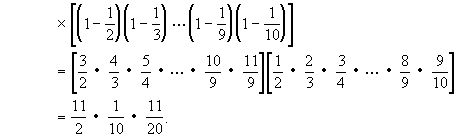
　通过以上例题可以看到，用字母表示数给我们的计算带来很大的益处．下面再看一个例题，从中可以看到用字母表示一个式子，也可使计算简化．

　例10 计算：

我们用一个字母表示它以简化计算．

1．括号的使用　

　在代数运算中，可以根据运算法则和运算律，去掉或者添上括号，以此来改变运算的次序，使复杂的问题变得较简单．

　例1 计算：

　分析 中学数学中，由于负数的引入，符号“+”与“-”具有了双重涵义，它既是表示加法与减法的运算符号，也是表示正数与负数的性质符号．因此进行有理数运算时，一定要正确运用有理数的运算法则，尤其是要注意去括号时符号的变化．

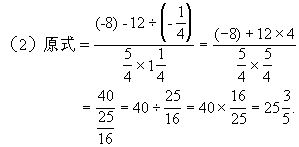
　注意 在本例中的乘除运算中，常常把小数变成分数，把带分数变成假分数，这样便于计算．

　例2 计算下式的值：

　211×555+445×789+555×789+211×445．

　分析 直接计算很麻烦，根据运算规则，添加括号改变运算次序，可使计算简单．本题可将第一、第四项和第二、第三项分别结合起来计算．

　解 原式=(211×555+211×445)+(445×789+555×789)

　　 　=211×(555+445)+(445+555)×789

　　 　=211×1000+1000×789

　　 　=1000×(211+789)

　　 　=1 000 000．

　说明 加括号的一般思想方法是“分组求和”，它是有理数巧算中的常用技巧．

　例3 计算：S=1-2+3-4+…+(-1)ⁿ⁺¹·n．

　分析 不难看出这个算式的规律是任何相邻两项之和或为“1”或为“-1”．如果按照将第一、第二项，第三、第四项，…，分别配对的方式计算，就能得到一系列的“-1”，于是一改“去括号”的习惯，而取“添括号”之法．

　解 S=(1-2)+(3-4)+…+(-1)ⁿ⁺¹·n．

　下面需对n的奇偶性进行讨论：

　当n为偶数时，上式是n／2个(-1)的和，所以有

　当n为奇数时，上式是(n-1)／2个(-1)的和，再加上最后一项(-1)ⁿ⁺¹·n=n，所以有

　例4 在数1，2，3，…，1998前添符号“+”和“-”，并依次运算，所得可能的最小非负数是多少？

　分析与解 因为若干个整数和的奇偶性，只与奇数的个数有关，所以在1，2，3，…，1998之前任意添加符号“+”或“-”，不会改变和的奇偶性．在1，2，3，…，1998中有1998÷2个奇数，即有999个奇数，所以任意添加符号“+”或“-”之后，所得的代数和总为奇数，故最小非负数不小于1．

　现考虑在自然数n，n+1，n+2，n+3之间添加符号“+”或“-”，显然

n-(n+1)-(n+2)+(n+3)=0．

　这启发我们将1，2，3，…，1998每连续四个数分为一组，再按上述规则添加符号，即

(1-2-3+4)+(5-6-7+8)+…+(1993-1994-1995+1996)-1997+1998=1．

　所以，所求最小非负数是1．

　说明 本例中，添括号是为了造出一系列的“零”，这种方法可使计算大大简化．

28、(本题10分)

(1)________　　　 ；(2)________　　　 ；(3)________　　　 ；

(4)去掉经理的工资后,其他员工工资的平均数是________　　 元，是否也能反映

该餐厅员工工资的一般水平?为什么?

27、(本题10分)

26、(本题8分)