0.9(80-x)+0.4x≤52

∴　 40≤x≤44；　　

　　 ∵x的取值范围是40、41、42、43、44，又y=50x+45(80-x)，即y=5x+3600。

　　 由观察知：当x=44时，y有最大值，最大值为5x44+3600=3820，即当N型号的时装为44套时，所获利润最大，最大利润为3820元　　

　 教师：你遇到过下面的情况吗?用所学的知识来解决。

0.9(80-x)+0.4x≤52

∴　 40≤x≤44；　　

　 　∵x的取值范围是40、41、42、43、44，又y=50x+45(80-x)，即y=5x+3600。

　　 由观察知：当x=44时，y有最大值，最大值为5x44+3600=3820，即当N型号的时装为44套时，所获利润最大，最大利润为3820元　　

　 教师：你遇到过下面的情况吗?用所学的知识来解决。

　 问题15：某学校需刻录一批教学用的VCD光盘，若电脑公司刻录，每张需9元(包括空白VCD光盘费)；若学校自刻，除租用刻录机需120元外，每张还需成本4元(包括空白VCD光盘费)。问刻录这批VCD光盘，到电脑公司刻录费用省，还是自刻费用省?请说明理由。

　 教师：同学们仍然分组讨论交流。

　 设需刻录x张VCD光盘，则到电脑公司刻录需9x元，自刻需要(120+4x)元。

　当9x>120+4x时，即x>24时，自刻费用省。　　

　 当9x=120+4x时，即x=24时，到电脑公司与自刻费用一样。

　 当9x<120+4x时，即x<24时，到电脑公司刻录费用省。

　 教师：好．下面你能提出一个你所遇的实际问题吗?请大家来一起解决。　

　 例

　 问题16：一个长方形足球场的长为xm，宽为70m；如果它的周长大于350m，面积小于7560，求x的取值范围，并判断这个球场是否可以用作国际足球比赛o

　 (注：用于国际比赛的足球场的长在100m到110m之间，宽在64m到75m之间)　　

　 (教师仍根据学生的实际情况，灵活处理)　　

　 参考解：依据长方形的周长和面积公式，得

　　　　　 2(x+70)>350，　　 ①

　　 　　　70x < 7560　　　 ②

　 解：①得x>105，解②得x<108．

　　　 ∴ 105<x<108．

　 根据国际比赛足球场的要求，该球场可以用作国际足球比赛。

　 问题3：假如你是一位具有环境意识的企业家，决策者，你该怎么办？

为了保护环境，某企业决定购买10台污水处理设备，现有A、B两种型号的设备，其中每台的价格、月处理污水量及年消耗费如下表：

　　 经预算，该企业购买设备的资金不高于105万元o

　 (1)请你设计该企业有几种购买方案；　　

　 (2)若企业每月产生的污水量为2040吨，为了节约资金，应选择哪种购买方案。　　

　 教师：请同学们分组讨论，再请同学来交流o　　

　 分析：如果设购买A型污水处理设备x台，则购买B型设备为(10－x)台，那么可以用含x的代数式表示购买设备的资金总额为12x+10(10-x)万元。“不高于”即为“≤”，可列出不等式来解。

　 解：(1)设购买A型污水处理设备x台，则购买B型设备(10-x)台，由题意知　　

　 　12x+10(10-x)≤105，x≤2．5

　 ∵x取非负整数，∴x可取0、1、2．

　 ∴有三种不同购买方案，购A型0台，B型10台；购A型1台，B型9台； 购A型2台，购B型8台。

(2)由题意得240x+200(10-x)≥2040．

解得　 x≥l

　　 ∵x≥l，∴x取l或2．

　 X=1时，购买资金为　 12xl+10x9=102(万元)；

　 当x=2时，购买资金为　 　12x2+10x8=104(万元)o

　 ∴为了节约资金，应选购A型1台，B型9台。

　 问题4：某服装厂现有A种布料70米、B种布料52米，现计划用这两种布料生产M、N两种型号的时装共80套，已知做一套M型号时装需要用A种布料0．6米、B种布料0．9米，可获利润45元，做一套N型号的时装需要用A种布料1．1米、 B种布料0．4米，可获利润50元，请你设计最佳方案。　　

　 (教师可根据学生的实际情况灵活处理) 我们可以将问题转化为一元一次不等式组的问题来求解。

　　 (参考解：设生产N型号的时装套数为x，用这批布料生产这两种型号的时装 所获的总利润为y元，根据题意　　

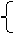　　　 0.6(80-x)+1.1x≤70,　　　　

0.57　 + 0.35 X ≧ 0.45X……… 2分

解这个不等式，得：X≧5.7　 因为参加的人数只能是整数,所以参加的人数至少是6人。……… 1分

答：参加合影的同学至少有6人。……… 1分

11:学生若干人，住若干宿舍，如果每间住4人，那么还有18人没有宿舍住；如果每间住6人，那么有一间宿舍没住满，求该校住宿人数和宿舍间数。

问题:12:　 甲.乙两家商店出售同样的茶壶和茶杯,茶壶每只定价都是20元,茶杯每只定价都是5元.两家商店的优惠办法不同:甲商店是购买1只茶壶赠送1只茶杯;乙商店是按售价的确92%收款.某顾客需购买4只茶壶.若干只(超过4只)茶杯,去哪家商店购买优惠更多?　



13:某工程队计划在10天内修路6千米,施工前2天修完1.2米后,计划发生变化,准备提前2天完成修路任务,以后几天平均每天至少要修路多少千米?

问题14：某服装厂现有A种布料70米、B种布料52米，现计划用这两种布料生产M、N两种型号的时装共80套，已知做一套M型号时装需要用A种布料0．6米、B种布料0．9米，可获利润45元，做一套N型号的时装需要用A种布料1．1米、 B种布料0．4米，可获利润50元，请你设计最佳方案。　　

　 (教师可根据学生的实际情况灵活处理) 我们可以将问题转化为一元一次不等式组的问题来求解。

　　 (参考解：设生产N型号的时装套数为x，用这批布料生产这两种型号的时装 所获的总利润为y元，根据题意　　

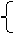　　　 0.6(80-x)+1.1x≤70, 　　　　

0.05X>7.5

　　 系数化为1,得

　　　　　　 X>150

　　 答:累计购物超过150元时在甲店购物花费小

问题9　

小兰准备用30元买钢笔和笔记本，已知一支钢笔4.5元，一本笔记本3元。

(1)她买了5本笔记本，则她最多还可以买多少支钢笔？

(2)钢笔和笔记本共8件，则她最多可以买多少支钢笔？

(3)如果她钢笔和笔记本共买了8件，则她有多少种购买方案？

10:某班同学外出春游，需拍照合影留念；若一张底片需0.57元，冲印一张需0.35元，每人预定得到一张而且出钱不超过0.45元，问参加合影的同学至少有几人？

　答案(不是唯一的，仅作参考)及评分标准：

解：设参加合影的同学至少有X人，根据题意，得：……… 1分

7.有10名菜农，每人种甲种蔬菜3亩或乙种蔬菜2亩，已知甲种蔬菜每亩可收入0.5万元，乙种蔬菜每亩可收入0.8万元。若要使菜农的总收入不低于15.6万元，则最多只能安排多少人种甲种蔬菜？

问题8:

　　 甲、乙两商店以同样价格出售同样的商品，并且又各自推出不同的优惠方案：在甲店累计购买100元商品后，再购买的商品按原价的90%收费；在乙店累计购买50元商品后，再购买的商品按原价的95%收费。顾客怎样选择商店购物能获得更大优惠？

首先考虑一下：

甲商店优惠方案的起点为购物款达 　　　　　元后；

乙商店优惠方案的起点为购物款达 　　　　　元后

(1)现在有4个人，准备分别消费40元、80元、140元、160元，那么去哪家商店更合算？为什么？

(2)如果累计购物超过100元，那么在甲店购物花费小吗？　 　

(3)累计购物超过100元而不到150元时，在哪个店购物花费小？累计购物恰好是150元时，在哪个店购物花费小？

　 (4)根据甲乙商店的销售方案，顾客怎样选择商店购物能获得更大优惠？你能为消费者设计一套方案吗？

解：设累计购物X元(X＞100)，如果在甲店购物花费小，则

　　50+0.95(X-50)>100+0.9(X-100)

　 去括号得

　　　　　 50+0.95X-47.5>100+0.9X-90

　 移项且合并,得

6．某单位计划在新年期间组织员工到某地旅游，参如旅游的的人数估计为10~25人，甲、乙两家旅行社的服务质量相同，且报价都是每人200元，经过协商，甲旅行社表示可给予每位游客七五折优惠；乙旅行社表示可先免去一位游客的旅游费用，其余游客八折优惠，该单位选择哪一家

旅行社支付的旅游费用较少？

5、某园林的门票每张10，一次使用。考虑到人们的不同需求，也为了吸收更多的少游客，该园林除保留原有的售票方法外，还推出了一种“购买个人年票”的售票方法(个人年票从购买日起，可供持票者使用一年)。年票分A、B、C三类：A类年票每张120元，持票者是入该园林时，无需再购买门票；B类门票每张60元，持票者进入该园林时，需再购买门票，每次2元；C类门票每张40元，持票者进入该园林时，需再购买门票，每次3元。(1)如果您只选择一种购买门票的方式，并且您计划在一年中花80元在该园林的门票上，试通过计算，找出可使进入该园林的次数最多的购票方式。(2)求一年中进入该园林至少超过多少次时，购买A类年票比较合算。

2、a取什么值时，代数式4a+2的值：

(1)大于1？　　　 (2)等于1？　　　 (3)小于1？

问题3：学校举行的“我与法”的知识竞赛中共有20道题．对于每一道题，答对了得10分，答错或不答扣5分．至少要答对几道题，其得分不少于80分? (列出算式，不要求求解)

　 　你能解决吗?分组讨论．

　 　分析：列表如下

根据上列分析可列出不等式为:_________________________---80．

问题4：一个工程队原定10天内至少要挖掘600m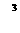的土方，在前两天共完成了120m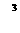后，又要求提前2天完成挖掘土方任务，问以后几天内，平均每天至少要挖掘多少土方?(列出算式，不要求求解)。　　

根据列表分析可列出不等式为__________________≥600．

1、用不等式表示：

1)b不是正数：　　　　 　　　　 　； b是非负数：　　　　　　　　 ；

x的一半小于－1　 ：　　　　　　 ；y与4的和大于0.5：　　　　 。

(2)x的2倍大于x：　　　　 (3)y的与3的差是负数：　　　　

(4)3Y与7的和的四分之一小于-2：　　　　 　　　　　　　

(5)a与b的差是非负数：　　　　　　　　

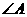29．(1)如图1，在中，O为和平分线BO、CO的交点，则与有怎样的关系？为什么？(3分)

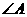(2)如图2，在中，和的角平分线相交于点O，则与有怎样的关系？为什么？(3分)

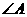(3)如图3，在中，和的外角平分线相交于点O，那么你发现与有怎样的关系？为什么？(4分)