
题目列表(包括答案和解析)
3、方程 的解是_______,根是_______。
的解是_______,根是_______。
2、下面的方程变形中,(1)2x+6=-3,变形为2x=-3+6;
(2)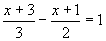 ,变形为2x+6-3x+3=6;(3)
,变形为2x+6-3x+3=6;(3) ,变形
,变形
为6x-10x=5;(4) ,变形为3x=10(x-1)+1,正确的是_______。
,变形为3x=10(x-1)+1,正确的是_______。
(只填代号)
1、下列各式(1)1+5=6;(2)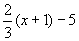 ;(3)2(x+1)=3x-4中,_______
;(3)2(x+1)=3x-4中,_______
是等式;_______是方程(只填代号)。
28.(本小题12分)
如图,用同样规格的黑白两色的正方形瓷砖铺设矩形地面,请观察下列图形并解答有关问题。

(1)在第n个图中,第一横行共_______块瓷砖,第一竖列共有_______块瓷砖。(均用含n的代数式表示)(2分)
(2)设铺设地面所用瓷砖的总块数为y,请写出y与(1)中的n的函数。(2分)
(3)按上述铺设方案,铺一块这样的矩形地面共用了506块瓷砖,求此时n的值。(4分)
(4)是否存在黑瓷砖与白瓷砖块数相等的情形?请通过列方程计算说明理由。(4分)
27.(本小题10分)
如图27-1,已知 为正方形
为正方形 的对角线
的对角线 上一点(不与
上一点(不与 重合),且四边形
重合),且四边形 也是正方形
也是正方形
(1) 求证: .(4分)
.(4分)
(2) 如图27-2,试选取正方形 的两个顶点,分别与正方形
的两个顶点,分别与正方形 的两个顶点连结,使得到的两条线段在正方形
的两个顶点连结,使得到的两条线段在正方形 绕点
绕点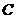 按逆时针方向旋转的过程中长度始终相等,并证明你的结论 .(6分)
按逆时针方向旋转的过程中长度始终相等,并证明你的结论 .(6分)


26、(本小题10分)
某农场去年种植了10亩地的南瓜,亩产量为2000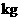 ,根据市场需要,今年该农场扩大了种植面积,并且全部种植了高产的新品种南瓜,已知南瓜种植面积的增长率是亩产量的增长率的2倍,今年南瓜的总产量为60 000kg,求南瓜亩产量的增长率.
,根据市场需要,今年该农场扩大了种植面积,并且全部种植了高产的新品种南瓜,已知南瓜种植面积的增长率是亩产量的增长率的2倍,今年南瓜的总产量为60 000kg,求南瓜亩产量的增长率.
25、(本小题10分)某工厂生产的某种产品按质量分为1 0个档次.第1档次(最低档次)的产品一天能生产7 6件,每件利润10元.每提高一个档次,每件利润增加2元,但一天产量减少4件.若生产某档次的产品一天的总利润为1080元,求该产品的质量档次.
24.(本小题10分)在一幅长8分米,宽6分米的矩形风景画(如图①)的四周镶宽度相同的金色纸边,制成一幅矩形挂图(如图②).如果要使整个挂图的面积是80平方分米,求金色纸边的宽.


23、 (本小题8分)如图,在所给网格图(每小格均为边长是1的正方形)中完成下列各题:
(本小题8分)如图,在所给网格图(每小格均为边长是1的正方形)中完成下列各题:
(1)作出格点 关于直线DE对称的
关于直线DE对称的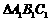 ;(2分)
;(2分)
(2)作出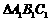 绕点
绕点 顺时针方向旋转90°后的
顺时针方向旋转90°后的 ;(3分)
;(3分)
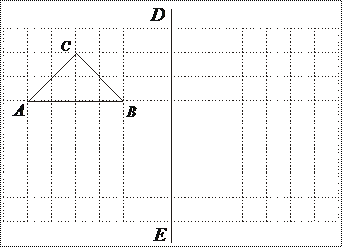 (3)求
(3)求 的周长.(3分)
的周长.(3分)
22、解下列方程(12分)
(1) (2)
(2)
(3)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com