3、　　　　 执行计划：把已制订的计划具体地进行实施；

2、　　　　 制订计划：在理解问题的基础上，运用有关的数学知识

和方法拟订出解决问题的思路和方案；

1、　　　　　　 理解问题：弄清问题的意思，以及问题中涉及的术语、词

汇的含义；分清问题中的条件和要求的结论等；

0.　　 04×60×60÷6=24元〈30元，说明通话时间超过1小时，由题意得：

3600+×6=×6

解得：x=24(元)

答：调整后的话费为24元。

[说明：此题应给学生较充分的时间，在学生独立完成后，再在小组内交流、补充，最后组织学生完成这个问题。通过这一环节培养学生勇于探索，认真细致的精神。]

归纳小结：

师：通过刚才对此例的问题解决，请大家认真回顾，细细体会，说出把一个实际问题转化为数学问题来解决的基本步骤是怎样的？

(让学生畅所欲言，最后归纳总结出以下步骤，屏幕显示)

3、调整前或调整后这个电话的通话的时间不变。

[这一层次及时鼓励学生通过观察、分析、小组讨论，找出其中的等量关系，并尝试用文字语言表述出来，有利于提高学生的分析问题的能力和语言表达能力]

师：根据刚才的分析，你能利用方程来解决这个问题吗？

　 (学生独立完成，老师巡视，找出典型的在实物投影仪上讲评)

解：设所求的话费为x元，

(×6=510秒〈3600秒，说明这个电话始终在20：00-22：00时间段内〉由题意得：

×6=×6

解这个方程得：x=2.55(元)

答：这个电话在调整后的话费是2.55元。

说明：①括号内部分估计多数学生不会想到，或已经想到但没有写出来，所以老师在讲评时，也先不出示这部分，然后让学生通过认真思考，补充完整；

②学生可能会得到不同形式的方程，但只要学生得到的方程是合理的，教师都应给予肯定和鼓励。

〈应用与拓展〉：

(1)　　 如果在21：00时拨打的这个电话，通话时间为75分钟，则调整前后的话费分别是多少？

调整前：×0.04+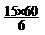×0.03=24+4.5=28.5(元)

调整后：×0.03=22.5(元)

[说明：此题可先让学生思考后得出应该分段计算]

(2)　　 如果本例中调整前的话费为30元，则调整后的话费是多少？

解：设调整后的话费为x元，

2、基本关系：通话时间×话费标准=话费；

1、涉及到通话时间、话费标准和话费三个基本量；

2、小明到希望书店帮同学们购书，售货员告诉他，如果用20元钱办“希望书店会员卡”，将享受八折优惠，请问在这次买书中，小明在什么情况下，办会员卡与不办会员卡一样？当小明买标价为200元的书时，怎么合算，能省多少钱？

师：同学们，你们打过电话吗？付过电话费吗？你们付的电话费是怎样计费的？(在学生回答完上述问题后，出示下表)：

　 　中国电信杭州分公司2002年调整后的201卡普通国内长话资费标准如下：

师：你能理解这个表格吗？根据这个表格，你能解决什么问题？请举例说明。(这里的问题是开放性的，有利于激活学生的思维，估计学生会说一些比如：调整后在09：00-18：00时间段内打了15分钟电话，就可以算出话费为9元，等等，然后老师给出下面问题)

问题：某人在21：00时拨打一个从杭州到上海的电话，如果调整前的话费为3.4元，那么这个电话在调整后的话费是多少？

[这一层次从学生熟悉的生活经历出发，选择学生身边的、感兴趣的“打电话”“付电话费”，给学生提出有关的数学问题，唤起学生的求知欲]

1、据了解，个体服装店销售衣服只要高出进价的20%便可盈利，但老板们常以高出进价50%－100%标价，假如你准备买一件标价为200无的服装，应在什么范围内还价。

5、某车间有原料40千克，乙种原料36千克，利用这些原料生产A、B两种产品共5件，已知一件A产品需甲种原料9千克，乙种原料3千克，可获利润700元；一件B种产品需甲种原料4千克，乙种原料10千克，可获利润1200元，设生产A种产品X件。

(1)列式表示：

生产B种产品的件数　　　　　　。

两种产品共用甲种原料的千克数　　　　　　。

两种产品共用乙种原料的千克数　　　　　　

(2)请你设计：A、B两种产品的件数有哪几种方案(就是5件产品中，A、B各几件)？并简要理由。

(3)用X的式子表示这批产品所获利润，你所设计的方案中，哪种方案利润最大？最大利润是多少？