1. 解：设甲的速度为x公里/小时，乙的速度为y公里/小时，则根据题意：

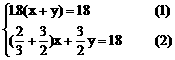
　　 解之得：

27从甲地到乙地，先下山后走平路，某人骑自行车从甲地以每小时12千米的速度下山，而以每小时9千米速度通过平路，到乙地55分钟。他回来时以每小时8千米的速度通过平路，而以每小时4千米速度上山，回到甲地用小时，求甲、乙两地的距离。

　　 分析：

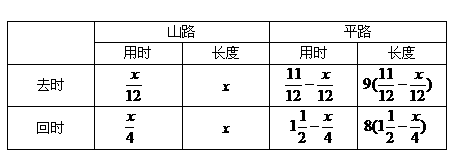
　　 根据“去时所走平路长=回时所走平路长”列方程求解。

　　 解：设山路长为x千米，依题意列方程为：

　　 解这个方程，得。

　　 代入方程左边，算得平路长为：

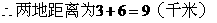
　　 答：甲乙两地距离为9千米。

28甲、乙两人在周长是400米的环形跑道上散步．若两人从同地同时背道而行，则经过2分钟就相遇．若两人从同地同时同向而行，则经过20分钟后两人相遇．已知甲的速度较快，求二人散步时的速度．(只列方程，不求出)

分析：这个问题是环形线上的相遇、追及问题．其中有两个未知数：甲、乙二人各自的速度．有两个相等关系，即

(1)背向而行：两次相遇间甲、乙的行程之和=400米；

(2)同向而行：两次相遇间甲、乙的行程之差=400米．

(让学生自己设未知数，列方程组，教师请一名学生将自己所列的方程组写在黑板上．)

解：设甲人速度为每分钟x米，乙人速度为每分钟行走y米．依题意，得

29人骑自行车绕800米长的环形跑道行驶，他们从同一地点出发，如果方向相反，每1分20秒相遇一次．如果方向相同，每13分20秒相遇一次．求各人的速度．

30某一铁路桥长1000米．现有一列火车从桥上通过，测得火车从开始上桥到完全过桥共用1分钟，整列火车完全在桥上的时间为40秒钟．求火车速度．

31地相距280千米，一艘轮船在其间航行．顺流用了14小时，逆流用了20小时．求这艘轮船在静水中的速度和水流速度

甲、乙两相距36千米两地相向而行，如果甲比乙先走2时，那么他们在乙出发2.5时后相遇；如果乙比甲先走2时，那么他们在甲出发3时后相遇，甲、乙两人每时各走多少千米？

解：设甲、乙两人每小时分别行走x千米、y千米。根据题意可得：

　 4.5x+2.5y=36　　　　　　　　　　　 x= 6

　 3x+5ky=36　　　 解此方程可得　 ：　 y=4

所以甲每小时走6千米，乙每小时走4千米。

32乙两码头相距60千米，某船往返两地，顺流时用3小时，逆流时用4小时，求船在静水中的航速及水流速度。②

　 分析：复习船在顺流航行及逆流航行中的速度与船在静水中的速度、水流速度的关系。

　 顺流航行的船速=在静水中的船速度+水流速度

　 逆流航行的速度=在静水中的船速度-水流速度

　 师生共同分析两个相等关系

⑴　 顺流航行的速度×3=60千米

⑵　 逆流航行的速度×4=60千米

解：设船在静水中的速度为x千米／时，水流速度为y千米／时。

　 由题意得　　　　 3(x+y)=60　 ①

　　　　　　　　　 4(x-y)=60　 ②

解这个方程组;得

　　　　 x=17.5

　　　　 y=2.5

　　　　　 答：略

　 练习：P48　 7.

25、乙两相距6千米，两人同时出发，同向而行，甲3小时可追上乙；相向而行，1小时相遇，两人的平均速度各是多少？

解：设甲的平均速度是每小时行x千米，乙的平均速度是每小时行y，根据题意，得：　 3x=3y+6

　 x+y=6　　　　 解这个方程组，得：　　 x= 4

　　　　　　　　　　　　　　　　　　　 y=2

答：平均每小时甲行4千米，乙行2千米。

26乙两人从相距18千米的两地同时出发，相向而行，1小时48分相遇，如果甲比乙早出发40分钟，那么在乙出发1小时30分相遇，求甲、乙二人各自的速度。

4、本题的等量关系是什么？

如何列出一元一次方程？

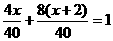
21种货物，连续两次均以10%的幅度降价后，售价为486元，则降价前的售价为____元。

22家商店里某种服装每件的成本价是50元，按标价的8折(即按标价的80%)优惠卖出。　 (1)、如果每件仍获利14元，这种服装的标价是多少元？

(2)、如果利润率为20%，这种服装的标价是多少元？商场将一件成本价为100元的夹克，按成本价提高50%后，标价150元，后按标价的8折出售给某顾客，请算一算，在这笔交易中商家有没有赚？学生计算，同桌之间交流后，教师提问检查：

150×80%-100=20(元)每件夹克商家赚了20元。

23商店积压了100件某种商品，为使这批货物尽快脱手，该商店采取了如下销售方案，将价格提高到原来的2.5倍，再作三次降价处理：第一次降价30%，标出“亏本价”；第二次降价30%，标出“破产价”；第三次降价30%，标出“跳楼价”。三次降价处理销售结果如下表：

(1)跳楼价占原价的百分比是多少？

(2)该商品按新销售方案销售，相比原价全部售完，哪一种方案赢利多？

24商品按定价销售，每个可获利45元，现在按定价的8.5折出售8个所能获得的利润与按定价每个减价35元出售12个所获得利润一样。问这种商品每个的进价、定价各是多少元？

思考题：(1)、据了解，个体服装销售只要高出进价的20%便可盈利，但老板常以高出进价的50%-100%标价。假如你准备买一件标价为200元的服装，应在什么范围内还价？

3、一个人独做4小时的工作量是多少？

2、由一个人独做要40小时完成，那么每人做1小时的工作量是多少？

3、某商品的进价为200元,标价为300元,打折销售时的利润为5%,此商品是按几折销售的?

20理一批图书，由一个人做要40小时完成，现在计算由一部分人先做4小时，再增加2人和他们一起做8小时，完成这项工作，假设这些人的工作效率相同，具体先安排多少人工作？

分析：1、这里把什么看作单位1；

2、某商场有一件商品需要降价处理，现把它降价25%后售价75元，设这件商品降价前的原价卖x元，列方程为　　　　　　　　　　　　　　 　　　　　　　　.

1、某商品的进价为150元,销售价为180元, 此商品的利润率是_________.

18、乙两队学生绿化校园，如果两队合作，6天可以完成；如果单独工作，乙队比甲队多用5天，两队单独工作各要多少天？

19一个水池装有甲、乙、丙三个进水管，单开甲管45分钟注满水池，单开乙管60分钟注满水池，单开丙管90分钟可注满水池。如果三管一齐开_________________________分钟注满水池。

说明：：：商家将一件成本是100元的夹克,按成本价提高50%后,标价150元,后按标价的8折出售给某顾客,请算一算,在这笔交易中商家有没有赚钱?

成本价___标价___售价____利润____利润率_______

将连续的偶2，4，6，8，…，排成如下表：

2　　 4　　 6　　 8　　 10

12　　 14　 16　　 18　　 20

22　　 24　 26　　 28　　 30

32　　 34　 36　　 38　　 40

　 …　　　　 …　　　　

(1)　　　 十字框中的五个数的和与中间的数和16有什么关系？(2分)

(2)　　　 设中间的数为x ，用代数式表示十字框中的五个数的和，(2)

(3)　　　 若将十字框上下左右移动，可框住另外的五位数，其它五位数的和能等于2010吗？如能，写出这五位数，如不能，说明理由。(2分)