7．(2004·青海)关于x的方程ax-3=0的根是2，则a=________。

6．(2004·玉林)若-m=4，则m=____________。

4．(2005.杭州市)如果,那么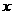等于:　 　　　　　　　　　　　　　 (　　 )

A．1814.55　 　　　　 B．1824.55 　　　　 C．1774.45　 　　　D．1784.45

示，那么“ A”、“　 ”、“　 ”这三种物体按质量从大到小的顺序排应为　　　　　 (　　 )

	B		A		C

C．　　　　　　　　　　 D．

3．在公式P=中，已知P、F、t都是正常数，则S等于　　　　　　　　　　　　　　　　　 (　　 )

　 　 A．　　　　 　　　 B．　　　　 　　 C．　　 　　　 D．PFt

2．(2001.陕西)如果2(x+3)的值与3(1-x)的值互为相反数，那么x 等于　　　　 (　　 )

　　 A．-8 　　　　　　　 B．8 　　　　　　　 C．-9　 　　　　　　 D．9

1．(2005.深圳市课改实验区)一件衣服标价132元，若以9折降价出售，仍可获利10%，则这件衣服的进价是　　　　　　 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　　 )

　　 A．106元　 　　　　　　 B．105元　 　　　　　　 C．118元　 　　　　　　 D．108元

3．根据方程ax=b的解的情况，求待定系数的值，如例6。

[典例精析]

例1：(2004.眉山)小李在解方程5a-x=13(x为未知数)时，误将－x看作+x，得方程的解为x=－2，则原方程的解为　　 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　　 )

　 　　 A．x=－3　 　　　　　　 B．x=0 　　　　　　　　　 C．x=2　　　　　 　 D．x=1

解析　 把x=2代入 5a+x=13(x为未知数)得5a+(－2)=13．所以a=3．再把a=3代人方程 5a-x=13，所以 x=2即可得到．　　　　　　　　　　　 答案：C

点评：依据方程解的定义，把方程的解代入原方程，转化为关于待定系数的方程。

例2：(2004.江苏无锡)设“○”、“□”、“△”分别表示三种不同的物体，用天平比较它们质量的大小，两次情况如图所示，那么每个“○”、“□”、“△”这样的物体，按质量从小到大的顺序排列为　　　　　　　　　　 (　　 )

A．○□△　　　　 B．○△□　

　C．□○△　　　　 D．△□○

解析　 由左图知：○＞□；由右图可得：□=2△。故选D．　　　　　　　　　 答案：D

例3：解方程2(x+3)－5(1－2x)=3(x+4)　　　　

分析　 此题含有括号，应以去括号开始来解方程

解：去括号，得2x+6－5+10x=3x+12，合并同类项，得12x+1=3x+12，

移项，得12x－3x=12－1，合并同类项，得9x=11，两边同时除以9，得x=.

点评：(1)去括号时，利用乘法分配律，千万不要漏乘某项，要特别注意是否需要变号；

　 (2)检验过程计算也要准确，否则也容易出错．

例4：(2003·黄州)解方程：.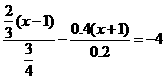

　分析：如果方程中的分子、分母含有小数，通常先将小数化为整数，再按一般步骤解方程;

　解　 原方程可化为 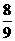(x-1)-2(x+1)=-4,　　 整理,得-5x=-5,　　 ∴x=1.　

　例5：　(2001·江苏)解方程：

分析：此题先用分配律简化方程，再解就容易了。

解：去括号，得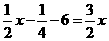　

　　 移项、合并同类项，得-x=6，　 系数化为1，得x=-6　

点评：解一元一次方程，掌握步骤，注意观察特点，寻找解题技巧，灵活运用分配律或分数基本性质等，使方程简化。

例6：已知关于x的方程无解，则a的值是　　　　　　　　　　　　　　 (　　 )

　　　 A．1　　　 　　　　　　 B．-1 　　　　　　　　 C．±1　　　　 　　　 D．不等于1的数

分析：需先化成最简形式，再根据无解的条件，列出a的等式或不等式，从而求出a的值。 解：去分母，得2x+6a=3x-x+6，　 即0·x=6-6a

　　 因为原方程无解，所以有6-6a≠0，　 即a≠1，　　　　　　　　　　　 答案：D

[常见误区]

解一元一次方程的常见的思维误区是：(1)移项不变号；(2)去分母时出现漏乘现象；(3)错把解方程的过程写成“连等”的形式；(4)去括号时出现漏乘或符号错误；(5)混淆分数的性质与等式的性质．

　[基础演练]

2．考查等式的基本性质以及一元一次方程的解法等类型题，如例2、例3、例4和例5。

1．有关等式、方程、一元一次方程的概念及方程解的应用等类型题，如例1。

3．掌握一元一次方程的解法，并能灵活应用.