
题目列表(包括答案和解析)
3.解下列方程:
(1) ;
(2)
;
(2) ;
;
(3) ; (4)
; (4) ;
;
(5) ;
(6)
;
(6)
2.填空题
(1)若关于 的方程
的方程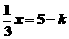 的解是
的解是 ,则
,则 _________.
_________.
(2)当 时,代数式
时,代数式 与
与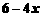 的值相等.
的值相等.
1.选择题
(1)下列方程变形正确的是( ).
A.由 得
得 B. 由
B. 由 得
得
C.由 得
得 D. 由
D. 由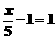 得
得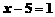
(2)下列方程后所列出的解不正确的是( ).
A. B.
B.
C.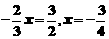 D.
D.
(3)方程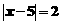 的解是( ).
的解是( ).
A.7 B. C.3 D.7或3
C.3 D.7或3
(4)一种书包经两次降价10%,现在售价 元,则原售价为( )元.
元,则原售价为( )元.
A.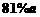 B.
B.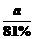 C.
C. D.
D.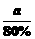
4.能根据具体情境中的数量关系,列出方程,解决简单的实际问题.
中招考点
一元一次方程概念及解法,一元一次方程的应用,能利用一元一次方程解决生活中的实际问题.
典型例题
例1解方程

解:去分母,得

去括号,得

移项、合并同类项,得 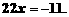
系数化为1,得
 .
.
说明:注意在解方程过程中正确进行有理数及整式的运算,步骤不宜过于简单.
例2
已知 是关于
是关于 的方程
的方程 的解,求
的解,求 的值.
的值.
分析:本题已知方程的解,要求方程中待确定的字母系数,可以像解数字系数的方程一样,先求出方程的解,再进行比较;也可以根据方程的解的定义:能使方程两边代数式的值相等的未知数的取值叫做方程的解,将 代入原方程,转化为关于
代入原方程,转化为关于 的方程求解.
的方程求解.
解1
解关于 的方程:
的方程:
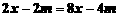 .
.
 .
.
 .
.
因为已知方程的解是 ,所以
,所以 ,即
,即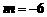 .
.
解2 因为 是方程的解,所以
是方程的解,所以
 .
.
解这个方程,得
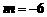 .
.
例3 列方程求下列问题的解:
(1)甲乙两车分别从相距360千米的两地相向开出,已知甲车速度是60千米/小时.乙车速度是40千米/小时.若甲车先开1小时,问乙车开出多少时间后两车相遇?
(2)小陈和老师一起整理了一篇教学材料,准备打印成稿.按篇幅估计老师单独打字需4个小时,小陈单独打字需6个小时,后来小陈先打了一个小时后,老师开始一起打.问还需多少小时完成?
分析:方程是刻画现实世界数量之间相等关系的一个重要数学模型,通过对实际问题中数量关系的分析,列出相关的代数式,进而建立方程,可以把复杂的实际问题转化为纯数学问题来解决.这一过程的关键是要透过纷繁多变的问题的表象,抓住数量关系的实质,抽象为数学问题.因此,常有面目迥异的情形,在学习中我们不能机械地记忆、套用某些题型而忽略了问题的本质.
像上述两个问题,不论是甲、乙两车还是师、生两人,主要的等量关系都是两个对象所完成数量的和等于总量,而其中一个对象所完成的数量又分为两部分;前一小时的和后来的.
请同学们注意强化训练第8题两个问题中数量关系和解法的比较.
解:(1) 设乙车开出 小时后两车相遇,根据题意,得
小时后两车相遇,根据题意,得
 .
.
解这个方程得
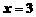 .
.
经检验,符合题意.
答 乙车开出3小时两车相遇.
(2)设老师开始打字后还需x小时完成,根据题意,得


解这个方程得

答 老师开始打字后还需要2个小时完成.
强化训练
3.掌握一元一次方程中移项、系数化为1等基本步骤,会解一元一次方程,
并会对方程的解进行检验.
2.理解方程变形的基本原理,能在解方程中正确应用.
1.解一元一次方程及其解的意义.
25.(本题8分)如图,直线y = kx+6与x轴y轴分别相交于点E,F.
点E的坐标为(- 8, 0), 点A的坐标为(- 6,0). 点P(x,y)是第二象限内的直线上的一个动点。
(1).求K的值;
(2).当点P运动过程中,试写出△OPA的面积S与x的函数关系式,并写出自变量x的取值范围;
(3).探究:当P运动到什么位置(求P的坐标)时,△OPA的面积为27/8,并说明理由

24.(5分)春、秋季节,由于冷空气的入侵,地面气温急剧下降到0℃以下的天气现象称为“霜冻”。由霜冻导致植物生长受到影响或破坏的现象称为霜冻灾害。
某种植物在气温是0℃以下持续时间超过3小时,即遭受霜冻灾害,需采取预防措施。下图是气象台某天发布的该地区气象信息,预报了次日0时-8时气温随时间变化情况,其中0时-5时,5时-8时的图像分别满足一次函数关系。请你根据图中信息,针对这种植物判断次日是否需要采取防霜冻措施,并说明理由。

23.(本题7分)某房地产开发公司计划建A、B两种户型的住房共80套,该公司所筹资金不少于2090万元,但不超过2096万元,且所筹资金全部用于建房,两种户型的建房成本和售价如下表:

(1)该公司对这两种户型住房有哪几种建房方案?
(2)该公司如何建房获得利润最大?
(3)根据市场调查,每套B型住房的售价不会改变,每套A型住房的售价将会提高a万元(a>0),且所建的两种住房可全部售出,该公司又将如何建房获得利润最大?
注:利润=售价-成本
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com