5．已知方程组，则m=_______，n=_______．

4．用加减消元法解方程组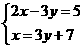正确的方法是(　 )

　　 A．①+②得2x=5　　 B．①+②得3x=12

　　 C．①+②得3x+7=5　 D．先将②变为x-3y=7③，再①-③得x=-2

3．用加减消元法解方程组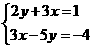，①-②得(　 )

　　 A．2y=1　　 B．5y=4　　 C．7y=5　　 D．-3y=-3

2．用加减消元法解方程组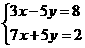 将两个方程相加，得(　 )

　　 A．3x=8　　 B．7x=2　　 C．10x=8　　 D．10x=10

1．对于方程组而言，你能设法让两个方程中x的系数相等吗？你的方法是_______；若让两个方程中y的系数互为相反数，你的方法是________．

4．解下列方程组:

　　 (1)　　　　　　　　

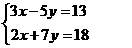
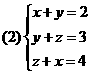
[典例分析]

　　 例1　 用加减法解方程组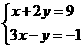

　　 思路分析：用加减法解二元一次方程组时，必须使方程组中①②两方程所含同一个未知数的系数相同或互为相反数．现在该方程组不具备这个条件，所以我们要想办法转化成这样的条件．方法一：观察x的系数：②中x的系数是①中的3倍，所以可得①×3，使x的系数相等，然后减去②，可消去x；方程二：观察y的系数：①中y的系数是②中的2倍，所以可将②×2，便y的系数互为相反数，再与①相加可消去y，两种方法皆可达到消元的目的．

　　 解：②×2，得6x-2y=-2　 ③

　　 ③+①得，7x=7,x=1

　　 把x=1代入①，得1+2y=9，2y=8，y=4

　　 所以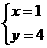是原方程组的解．

　　 方法点拨：用加减法解二元一次方程组时应当注意：

　　 ①当方程组比较复杂时，应先化简，如去分母、去括号、合并同类项等，将两方程化成ax+by=c的形式；

　　 ②当需将一未知数的系数扩大时，要根据等式的性质，一定要两边同乘以某一个倍数；

　　 ③在求出一未知数的值之后，可以将它代入化简后的方程组的任意一个方程中，求出第二个未知数的值；

　　 ④要想知道解是否正确，可将求得的解代入原方程组的两个方程加以检验．

　　 例2 　选择适合的方法解下列方程组：

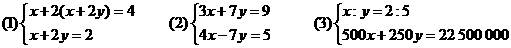
　　 思路分析：(1)方程组中，方程①中含有(x+2y)，因此，只需将方程②x+2y=2整体代入①即可化“二元”为“一元”．(2)方程组里两个方程中未知数y的系数互为相反数，因此只要两方程相加即可化“二元”为“一元”．(3)方程组中的第1个方程中两个未知数之间是比值关系，可化成x=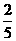y，然后代入②，用代入法求解；还可设x=2a，y=5a，将x=2a，y=5a代入②中，求得a的值，然后再分别代入x=2a，y=5a中，求得x、y的值，这样求解，可避免分数．

　　 解：(1)把②代入①得x+2×2=4，解之，得x=0

　　 把x=0代入②，得2y=2，解之，得y=1

　　 所以原方程组的解是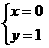

　 (2)①+②，得7x=14，解之，得x=2

　　 把x=2代入②得，8-7y=5，解之，得y=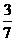

　　 所以原方程组的解是．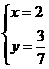

　　 (3)设x=2a，y=5a，并把它们代入②，得500×2a+250×5a=22 500 000

　　 解之，得a=10 000，

　　 把a=10000分别代入x=2a，y=5a中，得x=20 000，y=50 000

　　 所以原方程组的解是．

　　 方法点拨：代入法和加减法是解二元一次方程组的基本方法．以后解这种类型的题时，如果没有提出具体要求，应根据方程组的特别，选择其中一种比较简单的方法．选用解法时，一般是当其中某个未知数的系数为1(更特别的，像x=…)时，选用代入法较为简便；当两个方程中某个未知数的系数的绝对值相等或成整数倍时，选用加减法比较简便；其他情况，自己灵活运用．

[基础能力训练]

3．判断正误：

　(1)已知方程组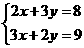则x、y的值都是负值　 (　 )

　 (2)方程组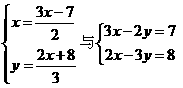有相同的解　 (　 )

　 (3)方程组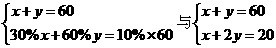解相同　 (　 )

2．自己总结出用加减法解二元一次方程组的一般步骤．

1．用加减法解二元一次方程组的关键是使方程组里两个方程中同一个未知数系数的绝对值_______，然后把方程两边分别相______或____，实现化二元为______，从而解出它的解．

8．用加减法解二元一次方程组．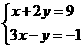

[点击思维]