3．若3x^m+1-5y^n-3=16是关于x、y的二元一次方程，则m=_____，n=_______．

2．若x^m+2y^|n|=5是二元一次方程，则m=______，n=_______．

1．下列方程中：①3x-2=y　 ②mn=8　 ③x+y=-6　 ④-4y=0　 ⑤3a=2

　　 其中是二元一次方程的是________(只填序号)．

3．一般地，一个二元一次方程有多少个解？

[典例分析]

　　 例1　 下列方程中，哪些是二元一次方程，哪些不是？

　　 (1)2x-3y+4=0　　　 (2)x+3y-2z=4　　　 　　(3)x²-y²=1

　　 (4)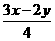=1　　　 (5)x=-z　　　　　　 (6)3ab=7

　　 思路分析：要想判断出一个方程是不是二元一次方程，必须紧卡二元一次方程的定义，即同时满足条件(1)含有两个未知数，(2)含有未知数的项的次数都是1的方程才叫做二元一次方程．并且注意“含有未知数的项的次数”不是“含有未知数的次数”这一点．

　　 解：(1)(4)是二元一次方程，(2)(3)(5)(6)都不是二元一次方程．

　　 方法点拨：做这种类型的题时，一定要分清方程中含有未知数的项的次数．像本例(5)中这一项的次数不是1，它是一个分式，整项的次数应是-1，故不是二元一次方程；还有(6)中ab这一项，它是一个单项式，它的次数应是a、b两字母的指数的和，故ab的次数是2，不是1，故也不是二元一次方程．记住这两个易出错的地方．

　　 例2　 对于下列每个方程，各求出它的一个正整数解．

　　 (1)x+3y=6　　　 (2)3x+2y=20

　　 思路分析：(1)先将方程x+3y=6变形为x=6-3y，要使方程有正整数解，y只能取1，才能保证x是正整数．于是方程x+3y=6的正整数解可求．

　　 (2)先将方程3x+2y=20，变形为y=10-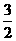x，要使方程有正整数解，只需x取正整数2、4、6，y即有正整数值．于是方程3x+2y=20的正整数解可求．

　　 解：(1)将方程x+3y=6变形，得x=6-3y

　　 令y=1时，则x=6-3×1=3

　　 故方程x+3y=6的正整数解为；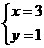

　　 (2)将方程3x+2y=20变形，得y=10-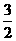x

　　 令x=2时，y=7

　　 故方程3x+2y=20的一个正整数解是．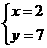

　　 方法点拨：解决本题的关键是先将两方程变形，即把其中的一个未知数用含有另一个未知数的代数式来表示．这是一项基本项，一定要表示对，这也是对以后学二元一次方程组的解法作准备的．

[基础能力训练]

2．方程+y=5及xy=3中x、y两个未知数的指数都是1，那这样的方程是不是二元一次方程呢？

1．你还记得“什么是方程”“什么是一元一次方程”吗？类比着来学习二元一次方程．

5．若x=4，y=1是二元一次方程mx-2y=4的解，则m=________．

点击思维

4．你能找出二元一次方程，2x-y=3的一个解吗？

3．使二元一次方程__________的值，叫做二元一次方程的一个解．

2．下列方程中，是二元一次方程的有(　 )个

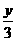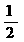　　 ①2x-y=1　 ②x+=3　 ③x²+x=2　 ④x²+y²=5　 ⑤5(x+y)=7(x-y)　 ⑥xy=-1

　　 A．1　　　 B．2　　　　 C．3　　　　 D．4