
题目列表(包括答案和解析)
2.3勾股定理的应用举例同步练习
第1题. 上午8:00,甲船从港口出发,以20海里/时的速度向东行驶,半个小时后,乙船也由同一港口出发,以相同的速度向南航行,上午10:00时,甲、乙两船相距多少远?
答案:解:如图所示.
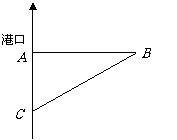 设甲、乙两船在10:00时,到达
设甲、乙两船在10:00时,到达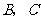 两点.
两点.
 海里,
海里,
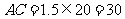 海里,
海里,
根据勾股定理,在 中
中
 .
.
 海里.
海里.
答:上午10:00时,甲、乙两船相距50海里.
第2题.  在我国古代数学著作《九章算术》中记载了一首有趣的问题,这个问题的意思是:有一个水池,水面是一个边长为10尺的正方形,在水池正中央有一根新生的芦苇,它高出水面1尺,如图所示.如果把这根芦苇垂直拉向岸边,它的顶端恰好到达岸边的水面.
在我国古代数学著作《九章算术》中记载了一首有趣的问题,这个问题的意思是:有一个水池,水面是一个边长为10尺的正方形,在水池正中央有一根新生的芦苇,它高出水面1尺,如图所示.如果把这根芦苇垂直拉向岸边,它的顶端恰好到达岸边的水面.
答案:解:设水深为 尺,则芦苇长为
尺,则芦苇长为 尺,
尺,
根据勾股定理得

芦苇的长度 (尺)
(尺)
答:水池深12尺,芦苇长13尺.
第3题. 甲乙两人从同一地点出发,甲以6m/s的速度向北走,乙以8m/s的速度向西跑,1min后,甲、乙相距离有多远?
答案:解:如图所示,设一分钟后,甲、乙分别走到 两点,
两点,

 ,
,
在 中,
中,
 根据勾股定理得
根据勾股定理得

 m.
m.
答:1min后,甲、乙两人相距600m.
第4题. 如图所示,长方形公园里要建一条小石子路,要求连结 两个景点,则石子路最短要多长?
两个景点,则石子路最短要多长?

答案:解:连结 ,根据勾股定理,在
,根据勾股定理,在 中,
中,

 m.
m.
 两点之间线段最短,
两点之间线段最短,
 最短路径为
最短路径为 .
.
答:石子路最短1000m.
第5题. 如图所示,一棱长为3cm的正方体上有一些线段,把所有的面都分成 个小正方形,其边长都为1cm,假设一只蚂蚁每秒爬行2cm,则它从下底面
个小正方形,其边长都为1cm,假设一只蚂蚁每秒爬行2cm,则它从下底面 点沿表面爬行至右侧
点沿表面爬行至右侧 点,最少要花几分钟?
点,最少要花几分钟?

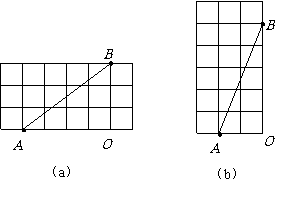
答案:解:如图所示,分两种情况:
(1)将正方体的正前、右侧两面展开,使 在同一平面内,
在同一平面内,
则 到
到 的最短路径是线段
的最短路径是线段 .
.
如图(a)所示, .根据勾股定理,
.根据勾股定理,
得
 5cm;
5cm;
(2)将正方体的正前,上底两面展开,使 在同一平面内,
在同一平面内,
则 到
到 的最短路径为线段
的最短路径为线段
如图(b)所示, .
.
根据勾股定理,得 .
.
比较上述两种情况(a)中 为最短路径,
为最短路径,
 s,
s,
 答:它至少要爬2.5s.
答:它至少要爬2.5s.
第6题. 如图所示,一根长90cm的灯管上,缠满了彩色丝带,已知可近似地将灯管看做圆柱体,且底面周长为4cm,彩色丝带均匀地缠绕了30圈,问:丝带共有多长?

答案:解:如图所示,先分析一圈的情况,右侧为展开图.
由图可知:一圈的长度为长方形的对角线 .
.
长方形的长 为圆柱的底面周长.
为圆柱的底面周长.
 ,
,
 根据勾股定理,
根据勾股定理,
 ,
,
答:彩带共需1.5m.

第7题. 某船向正东方向航行,在 处望见某岛
处望见某岛 在北偏东
在北偏东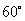 ,该船前进6海里到达
,该船前进6海里到达 点,则望见
点,则望见 岛在北偏东
岛在北偏东 ,已知在
,已知在 岛周围6海里内有暗礁,问若船继续向东航行,有无触礁的危险?并说明理由.
岛周围6海里内有暗礁,问若船继续向东航行,有无触礁的危险?并说明理由.
答案:解:由图知: 为直角三角形,
为直角三角形,
且 ,
,
 为直角三角形,
为直角三角形,
 且
且 ,
,
 ,
,
即 ,
,
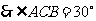 .
.
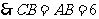 海里.
海里.
在 中,
中,

 .
.
 3海里.
3海里.
根据勾股定理,得
 .
.
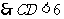 海里.
海里.
 若船继续向东航行,有触礁的危险.
若船继续向东航行,有触礁的危险.
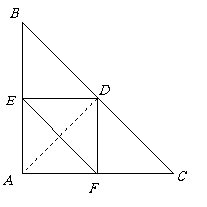
 第8题. 如图,
第8题. 如图,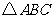 是等腰直角三角形,
是等腰直角三角形, 是斜边
是斜边 的中点,
的中点, 分别是
分别是 边上的点,且
边上的点,且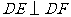 ,若
,若 .
.
求线段 的长.
的长.
答案:解:连结
 ,
,
又 为
为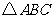 的中线,
的中线,
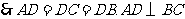 .
.
且 .
.
 ,
,
又 ,
,

同理: .
.
在 中,根据勾股定理得
中,根据勾股定理得

第9题. 一根直立的桅杆原长25m,折断后,桅杆的顶部落在离底部的5m处,则桅杆断后两部分各是多长?
答案:解:如图所示,根据题意,
 .
.
设 ,则
,则 ,
,
 根据勾股定理
根据勾股定理


答:桅杆折断后的两部分分别为12,13.
第10题. 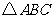 中,
中, ,中线
,中线 ,则
,则 .
.
答案:13
 第11题. 有一圆柱形罐,如图,要以
第11题. 有一圆柱形罐,如图,要以 点环绕油罐建梯子,正好到
点环绕油罐建梯子,正好到 点的正上方
点的正上方 点,则梯子最短需 米.(油罐周长12m,高
点,则梯子最短需 米.(油罐周长12m,高 m)
m)
答案:13
第12题. 如图,北部湾海面有一艘解放军军舰正在基地 的正东方向且距
的正东方向且距 地50海里的
地50海里的 处训练,突然接到基地命令,要该舰往
处训练,突然接到基地命令,要该舰往 岛,接送一名病危的渔民到基地医院救治,已知
岛,接送一名病危的渔民到基地医院救治,已知 岛在基地的北偏东
岛在基地的北偏东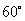 方向且距基地
方向且距基地 海里,又在
海里,又在 处的北偏西
处的北偏西 的方向上,军舰从
的方向上,军舰从 处出发,平均每小时行驶20海里,需要多少时间才能把患病渔民送到基地医院?
处出发,平均每小时行驶20海里,需要多少时间才能把患病渔民送到基地医院?

答案:解:由已知可知

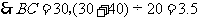 小时.
小时.
答:需3.5小时把患者送到.
第13题. 如图,有一个圆柱形油桶,它的高等于80分米,底面半径为25分米,在圆柱下底面圆周的 点有一只蚂蚁,它想吃到上底面与
点有一只蚂蚁,它想吃到上底面与 点在同侧的
点在同侧的 点的食物,但
点的食物,但 两点间有障碍,不能直接到达,蚂蚁只能沿桶壁爬行,则蚂蚁需爬行的最短路程是多少?(
两点间有障碍,不能直接到达,蚂蚁只能沿桶壁爬行,则蚂蚁需爬行的最短路程是多少?( 取整数3)
取整数3)
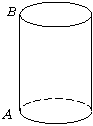
答案:解:圆柱侧面展开为矩形,长为 ,宽为80,
,宽为80,
最短距离为矩形对角线长,对角线长的平方 ,
,
 最短距离为170分米.
最短距离为170分米.
第14题. 某中学八年级学生想知道学校操场上旗杆的高度,他们发现旗杆上的绳子垂到地面还多1米,当他们把绳子的下端拉开5米后,发现下端刚好触地面,你能帮他们把旗杆的高度和绳子的长度计算出来吗?
答案:解:设旗杆高为 ,则绳长为
,则绳长为 ,
,
根据勾股定理, ,
,
 ,答:旗杆高为12米,绳长为13米.
,答:旗杆高为12米,绳长为13米.
第15题. 已知:如图,观察图形回答下面问题:
(1)此图形的名称为 ,
(2)请你与同伴一起做一个这样的物体,并把它沿 处剪开,铺在桌面上,研究一下它的侧面展开是一个 形.
处剪开,铺在桌面上,研究一下它的侧面展开是一个 形.
(3)如果点 是
是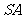 的中点,在
的中点,在 处有蜗牛想吃到的食品,恰好在
处有蜗牛想吃到的食品,恰好在 处有一只蜗牛,但它又不能直接爬到
处有一只蜗牛,但它又不能直接爬到 处,只能沿圆锥曲面爬行,你能画出蜗牛爬行的最短路程的图形吗?
处,只能沿圆锥曲面爬行,你能画出蜗牛爬行的最短路程的图形吗?
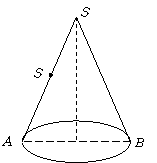 (4)圆锥的母线长为10cm,侧面展开图的夹角为
(4)圆锥的母线长为10cm,侧面展开图的夹角为 ,请你求出蜗牛爬行的最短路程的平方.
,请你求出蜗牛爬行的最短路程的平方.
答案:解:(1)圆锥 (2)扇形 (3) .
.
第16题. 四边形 中,
中, 各边长分别依次为
各边长分别依次为 ,且
,且 ,则四边形
,则四边形 的面积是 .
的面积是 .
答案:36
第17题. 等腰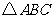 的底边
的底边 上有一点
上有一点 ,
, ,求等腰三角形腰长
,求等腰三角形腰长 及
及 的度数.
的度数.
答案:解:过 作
作 于
于 ,则有
,则有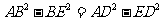 ,
,
 ,
,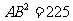 ,
,

 为等边三角形,
为等边三角形,
 .
.
第18题. 在同一个班上学的小明、小伟、小红三位同学住在 、
、 、
、 三个住宅区,如图所示,
三个住宅区,如图所示, 、
、 、
、 三点共线,且
三点共线,且 米,
米, 米,他们
米,他们
打算合租一辆接送车去上学,由于车位紧张,准备在此之间只设一个停靠点,
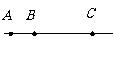 为使三位同学步行到停靠点的路程之和最小,你认为停靠点的位置应该设在 .
为使三位同学步行到停靠点的路程之和最小,你认为停靠点的位置应该设在 .
答案:点 处
处
第19题. 如图是一个长8m、宽6m、高5m的仓库,在其内壁的 (长的四等分点)处有一只壁虎、
(长的四等分点)处有一只壁虎、 (宽的三等分点)处有一只蚊子.则壁虎爬到蚊子处的最短距离为 m.
(宽的三等分点)处有一只蚊子.则壁虎爬到蚊子处的最短距离为 m.

答案: 或
或
21、下列图形中面积最大是( )
A.边长为5的正方形
B.半径为 的圆
的圆
C.边长分别为6,8,10的直角三角形 D.边长为7的正三角形
20、如果 的三边长
的三边长 满足关系式
满足关系式 ,则
,则 的三边分别为
的三边分别为 ,
, ,
, ,
, 的形状是 .
的形状是 .
19、 如图所示,铁路上 两站(视为直线上两点).相距25km,
两站(视为直线上两点).相距25km, 为两村庄(视为两个点),
为两村庄(视为两个点), 于
于 于
于 ,已知
,已知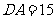 km,
km, km,现要在铁路
km,现要在铁路 上建设一个土特产收购站
上建设一个土特产收购站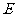 ,使得
,使得 两村庄到
两村庄到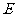 站的距离相等,则
站的距离相等,则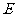 站应建在距
站应建在距 站多远处?
站多远处?

18、 已知:如图,四边形 中,
中, ,
, 与
与 相交于
相交于 ,且
,且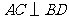 ,则
,则 之间一定有关系式:
之间一定有关系式: ,请说明理由.
,请说明理由.

17、已知 三边
三边 满足
满足 ,请你判断
,请你判断 的形状,并说明理由.
的形状,并说明理由.
16、有一个三角形的两边长是3和5,要使这个三角形成为直角三角形,则第三边边长的平方是 .
15、将直角三角形三条边的长度都扩大同样的倍数后得到的三角形( )
A.仍是直角三角形 B.可能是锐角三角形
C.可能是钝角三角形 D.不可能是直角三角形
14、下列三角形中,不是直角三角形的是( )
A.三角形三边分别是9,40,41;
B.三角形三内角之比为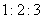 ;
;
C.三角形三内角中有两个互余;
D.三角形三边之比为 .
.
13、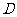 是
是 中
中 边上一点,若
边上一点,若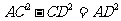 ,那么下列各式中正确的是( )
,那么下列各式中正确的是( )
A.
B.
C.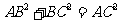
D.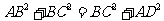
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com