

题目列表(包括答案和解析)
8. 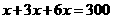 ;9.
;9. 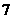 ;10. 108;
;10. 108;
1. D;2. A;3. B;4. A;5.(1)3x ,(2)4y,(3)-2y;6. 乘法分配律;7. 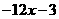 ;
;
3.2解一元一次方程(一)
22.图3-2-4是某超市中“漂柔”洗发水的价格标签,一售货员不小心将墨水滴在标签上,使得原价看不清楚,请你帮忙算一算,该洗发水的原价是( )
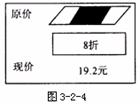 A.
A.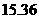 元
元
B.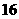 元
元
C.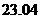 元
元
D.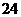 元
元
迷途知返
___________________________________________________________________________________________________________________________________________________________________________
课外精彩空间
数学危机--无穷小是零吗
18世纪,微分法和积分法在生产和实践上都有了广泛而成功的应用,大部分数学家对这一理论的可靠性是毫不怀疑的.
1734年,英国哲学家、大主教贝克莱发表《分析学家或者向一个不信正教数学家的进言》,矛头指向微积分的基础--无穷小的问题,提出了所谓贝克莱悖论.他指出:"牛顿在求xn的导数时,采取了先给x以增量0,应用二项式(x+0)n,从中减去xn以求得增量,并除以0以求出xn的增量与x的增量之比,然后又让0消逝,这样得出增量的最终比.这里牛顿做了违反矛盾律的手续──先设x有增量,又令增量为零,也即假设x没有增量."他认为无穷小dx既等于零又不等于零,召之即来,挥之即去,这是荒谬,"dx为逝去量的灵魂".无穷小量究竟是不是零?无穷小及其分析是否合理?由此而引起了数学界甚至哲学界长达一个半世纪的争论.导致了数学史上的第二次数学危机.
18世纪的数学思想的确是不严密的,直观的强调形式的计算而不管基础的可靠.其中特别是:没有清楚的无穷小概念,从而导数、微分、积分等概念也不清楚,无穷大概念不清楚,以及发散级数求和的任意性,符号的不严格使用,不考虑连续就进行微分,不考虑导数及积分的存在性以及函数可否展成幂级数等等.
直到19世纪20年代,一些数学家才比较关注于微积分的严格基础.从波尔查诺、阿贝尔、柯西、狄里赫利等人的工作开始,到威尔斯特拉斯、戴德金和康托的工作结束,中间经历了半个多世纪,基本上解决了矛盾,为数学
分析奠定了严格的基础.
21. 中国人民银行宣布,从2007年6月5日起,上调人民币存款利率,一年定期存款利率上调到3.06%.某人于2007年6月5日存入定期为1年的人民币5000元(到期后银行将扣除20%的利息锐).设到期后银行应向储户支付现金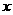 元,则所列方程正确的是( )
元,则所列方程正确的是( )
A.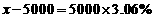
B.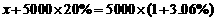
C.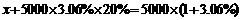
D.
20.[综合题]张欣和李明相约到图书城去买书.请你根据他们的对话内容(如图3-2-3),求出李明上次所买书籍的原价.

能力提高典题
19.[解决问题型题目]先观察,再解答.
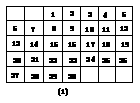
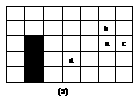
图3-2-2
如图3-2-2(1)是生活中常见的月历,你对它了解吗?
(1)图3-2-2(2)是另一个月的月历,a表示该月中某一天,b、c、d是该月中其它3天,b、c、d与a有什么关系?b=____;c=____;d=____.(用含a的式子填空).
(2)用一个长方形框圈出月历中的三个数字(如图3-2-2 (2)中的阴影),如果这三个数字之和等于51,这三个数字各是多少?
(3)这样圈出的三个数字的和可能是64吗?为什么?
18. [开放题]某商店有两种进价不同的计算器都卖64元,其中一个盈利60%,另一个亏本20%,
求:(1)它们的原价各为多少?
(2)各卖一个,商店是赔了,还是赚了?
17. [探究题]图3-2-1是一个数表,现用一个
|
矩形在数表中任意框出4个数 ,则
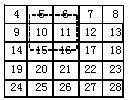
图3-2-1
(1)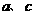 的关系是: ;
的关系是: ;
(2)当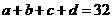 时,
时,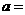 .
.
16.[易错题]已知关于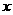 的方程
的方程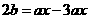 的解是
的解是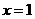 ,其中
,其中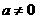 且
且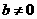 ,求代数式
,求代数式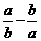 的值.
的值.
课标能力提升
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com