6、某校七年级(1)班有学生48人，一次数学测试的平均成绩约为83.24，下列问题，　　　

是准确数，　　　 是近似数，近似数精确到　　　 位。

5、鲁迅先生十分重视精神文化方面的消费，据史料记载，他在晚年用于购书的费用约占总收入的15.6%,则近似数15.6%有＿＿＿＿个有效数字.

4、据市统计局2005年公报，我市2006年人均生产总值约为14582元，则近似数14582的有效数字有　　　　 。

3、今年1-5月份，深圳市累计完成地方一般预算收入216.58亿元，数据216.58亿精确到__________。

2、由四舍五入法得到的近似数0.0200的有效数字是(　)

A．1个　　 B．2个　　 C．3个　　 D．4个

1、下列说法正确的有(　)．

①近似数0.05和近似数5.0的精确度相同;

②1.567精确到十分位后，有两个有效数字;

③近似数2000和近似数2.0×10³的精确度相同;

④近似数25.0和近似数2.50的有效数字的个数相同.

A．1个　B．2个　C．3个　D．4个

3.2 近似数随堂训练

1.7近似数练习

第1题. 计算，在计算器上显示得=5.841889，结果保留四个有效数字得≈_____，精确到百分位得≈_____．

第2题. 近似数0.00216精确到　　　　 ，有　　　　 个有效数字，它们是　　　　 ．

第3题. 一个近似数一般是通过_______法得到的，一般地一个近似数四舍五入到某一位，就说这个近似数____到哪一位．

第4题. 近似数5.03精确到________位，有________个有效数字，它们是________．

第5题. 据报载，到2003年6月底，我国累计报告爱滋病病毒感染者45092例，专家测算，我国爱滋病病毒感染者已达100万人，如不加强措施,_10年后这个数字可能超过1000万．这里，________是精确的，________________是近似的

第6题. 将圆周率π精确到0.1为_________，保留三个有效数字为________．

第7题. 做一件上衣需1.1米布，现有1.9米布可以做几件上衣？

第8题. 要把一根长2.3米的圆钢锯成每段长16.5厘米的一段一段加工零件，一共可以锯出几段?

第9题. 在一次立定跳远测验中，10名同学的成绩分别是(单位:米):1.63，1.85，1.64，1.71，1.53，1.64，1.38，1.66，1.75，1.81

(1)求他们的平均成绩；

(2)把平均成绩精确到0.1是多少?

(3)把平均成绩保留3个有效数字是多少?

第10题. 用四舍五入法，按括号中的要求对下列各数取近似值．

(1)349995(精确到百位)；(2)349995(精确到千位)

(3)3.4995(精确到0.01)；(4)0.003584(精确到千分位)

第11题. 下列问题中，哪些是近似数?哪些是精确数?

(1)地球半径是6371米；(2)一星期有7天；(3)光的速度是每秒30万千米； (4)我国古代的4大发明；(5)某学校有36个班级；(6)小明的体重是46.3公斤．

第12题. 球的体积计算公式为πR³，求半径为3.5cm的球的体积．(π取3.14，结果保留五个有效数字)

第13题. 下列由四舍五入得到的近似数精确到哪一位?各有几个有效数字?

①230；②18.3；③0.0098；④3.4万；⑤20.010．

第14题. 把两只半径分别为6.87cm和10.56cm的小铁球，熔化后铸成一只大铁球，已知每立方厘米铁重7.8克，求铸成的大铁球的重量(不计损耗，π取3.14，精确到克)．

第15题. 由四舍五入得到的近似数3.80，它表示大于或等于3.795，小于3.805，则近似数3.800表示的数的范围是什么？

第16题. 某班开家长会，预计有53名家长来，若每张凳子最多可坐3人，问至少要准备多少张凳子．

第17题. 正方体的棱长为62.68厘米，从中间挖出棱长为23.5厘米的小正方体，求余下的体积．(结果保留4个有效数字)

第18题. 计算，并把结果用科学记数法表示(保留2位有效数字)：

(1)3.6×10-1.2×10；　　　　　　　　　　　 (2)36××100．

第19题.我市今年参加中考的学生数为64397人，把这个数保留两个有效数字可记为　　　　　　　　　　　　 ．

4．你能比较两个数2002²⁰⁰³和2003²⁰⁰²的大小吗？

为了解决这个问题，我们首先把它抽象成数学问题，写出它的一般形式，即比较nn+1和(n+1)n的大小(n是自然数)。然后，我们从分析n=1，n=2，n=3，…这些简单情形入手，从中发现规律，经过归纳，猜想出结论。

(1)通过计算，比较下列各组中两数的大小(再空格中填写 “＞”、“＝”、“＜”).

①12　　 21； ②23　　 32； ③34　　 43； ④45　　 54； ⑤56　　 65；…

　 (2)从第(1)题的结果经过归纳，可以猜想出nn+1和(n+1)n的大小关系是：

　 (3)根据上面归纳猜想得到的一般结论，试比较下列两个数的大小：

　　　 2002²⁰⁰³　　　　 2003²⁰⁰²

5，如果一个正整数能表示为两个连续偶数的平分差，那么称这个正整数为“好

数”． 如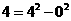：，，。因此4，12，20都是“好数”。

(1)28和2 012这两个数是“好数”吗？为什么？

(2)设两个连续偶数为2k+2和2k(其中k取非负整数)，由这两个连续偶数构造的好数是4的倍数吗？为什么？

(3)两个连续奇数的平方数(取正数)是好数吗？为什么？

3．已知a＝2，b＝－3。求代数式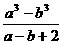的值。