7、一千个体积为1立方厘米的小正方体合在一起成为一个边长为10厘米的大正方体，大正方体表面涂油漆后再分开为原来的小正方体，这些小正方体至少有二面被油漆涂过的数目是多少个？

解：共有10×10×10＝1000个小正方体，其中没有涂色的为(10－2)×(10－2)×(10－2)＝512个，所以一面被油漆漆过的小正方体为(10－2)×(10－2)×6＝384　，所以至少有二面涂过的有1000－512－384＝104个。

也可以这样解决涂二面的有(10－2)×12＝96　，涂三面的有8个，所以共有96+8＝104个

6、甲、乙、丙、丁四人参加数学竞赛，赛后猜测他们之间的考试乘绩情况是：

甲说：“我可能考的最差。”

乙说：“我不会是最差的。”

丙说：“我肯定考的最好。”

丁说：“我没有丙考的好，但也不是最差的。”

成绩公布后，只有一人猜错了，则此四人的实际成绩从高到低的次序是__________。

解：甲不会错，

①假设乙错了，于是丙、丁正确，有“丙□□乙”；

②假设丙错了，于是为“…丙…丁…”，所以第一名只能是乙，于是为“乙丙丁甲”；

③假设丁错了，因为丙一定是最好的，所以丁只能是最后一句话错误，也就是说丁是最差的，“丙□□丁”。

即只能在②丙错误的情况下唯一确定为“乙丙丁甲”。

5、某小学六年级选出男生的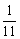和12名女生参加数学竞赛，剩下的男生人数是剩下的女生人数的2倍，已知这个学校六年级学生共有156人，则这个年级有男生__________人。

解：设有男生11x人，女生y人，那么有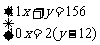，解得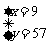，即男生有99人。

4、从1，2，3，…，30这30个自然数中，至少要取出__________个不同的数，才能保证其中一定有一个数是5的倍数。

解：其中不是5的倍数的数有30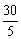－＝24个，于是只有选出25个数出来就能满足要求。

3、某自然数加10或减10，都是完全平方数，则这个自然数是__________。

解：设这个自然数为m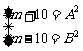，，A²－B²＝(A－B)×(A+B)＝20＝2²×5，

而(A－B)与(A+B)同奇同偶，所以只能是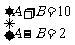，解得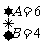，所以m＝6²－10＝26。即这个自然数为26。

2、有红、黄、蓝三面旗，把这些旗挂在一个旗杆上做成各种信号，如果按照挂旗的面数及从上到下颜色的顺序区分信号，那么利用这三面旗能表示__________种不同信号。(不算不挂旗情况)

解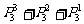：＝15种不同的信号。

1、定义“A☆B”为A的3倍减去B的2倍，即A☆B＝3A－2B，已知x☆(4☆1)＝7，则x＝__________。

解：3x－2(3×4－2×1)＝7，解得x＝9。

14、一个长方体的三个侧面面积是3、6、8平方厘米，这个长方体的体积等于多少立方厘米。

解：设长方体的三种棱长为a、b、c，体积为V。

有ab×bc×ca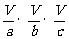＝＝＝＝V²，所以有3×6×8＝V²。

于是，长方体的体积为12立方厘米。

13、一个八位数，它被3除余1，被4除余2，被11恰好整除，已知这个八位数的前6位是257633，那么它的后两位数字是__________。

解：设这个八位数为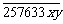，257633的数字和除以3的余数为2，所以x+y除以3的余数也是2。

奇数位数字和为5+6+3+y＝14+y，偶数位数字和为2+7+3+x＝12+x。有差为2+y－x(或x－y－2)，应为11的倍数。

，但是y-x＝9，只能是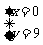不满足第2个式子。

或者，依次解为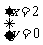、、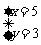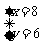。验证只有末两位为86，才有除以4的余数为2。

所以这个八位数的末两位为86。

12、如图有5×3个点，取不同的三个点就可以组合一个三角形，问可以组成＿＿＿＿个三角形。

解：如下图，任选三点有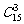＝455种选法，其中三点共线的有3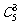+5+4×2＝30+5+8＝43。所以，可以组成三角形455－43＝412。